Інші властивості та різновиди графів

Ізоморфізм. Розглянемо три графа, що зображені на рис. 8.7

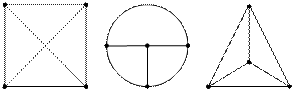
Рис. 8.7 Ізоморфні графи.

Ці графи мають різний геометричний вигляд, але при відповідному позначенні вершин та ребер дають однакові матриці інцидентності. Такі графи називаються ізоморфними.

Звідси можна також зробити висновок, що матриця інцидентності визначає граф без петель з точністю до ізоморфізму.

Прикладне застосування ізоморфізм графів находить в системах автоматизованого проектування (САПР), наприклад, при проектуванні горловин залізничних станцій.

Маршрути на графах. Часто розв’язання задач на графах потребує виявлення деякого маршруту з певними властивостями.

Визначення. Маршрут довжиною N – це послідовність m ребер графа, не обов’язково різних, але таких, що граничні вершини двох сусідніх ребер співпадають. Маршрут проходить через усі вершини, які інцидентні ребрам, що до нього належать.

Наприклад для псевдографа (рис. 8.4, а) маршрутом є послідовність (е₁, е₃, е₂, е₃, е₅). Замкнений маршрут закінчується у тій же вершині, з якої почався.

Маршрут, у якого всі ребра різні, називається ланцюгом, а - в якого всі вершини різні – простим ланцюгом.

Замкнений ланцюг називається циклом. Для псевдографа (рис. 8.4, а) - це послідовність ребер (е₂, е₃, е₄, е₅), а замкнений простий ланцюг утворює простий цикл, для псевдографа (рис. 8.4, а) - це послідовність (е₂, е₄, е₅).

Цикл, що містить всі ребра графа, називається ейлеровим циклом. Таким чином задача про кенінгсбергські мости зводиться до знаходження такого циклу. Простий цикл, що проходить через усі вершини графа, називають гамільтоновим циклом.

Для орграфів визначення маршруту аналогічне, але рух передбачається тільки у напрямку стрілок.

Зв’язність. Дві вершини графа називаються зв’язними, якщо існує маршрут, який поєднує ці вершини. Граф, будь яка пара вершин якого зв’язана, називається зв’язним. Зв’язність орграфів визначається аналогічно, тобто без врахування напрямку дуг. Специфічним для орграфа або замішаного графа є поняття сильного зв’язку. Орграф називається сильно зв’язаним, якщо для будь якої пари вершин υ_i та υ_j інує шлях як з υ_i до υ_j так і з υ_j до υ_i. Таким чином, граф, зображений на рис. 8.3, а, є сильно зв’язаним.

Очевидно, граф, що представляє план міста з однобічним рухом по деяких вулицях, повинен бути сильно зв’язаним, інакше знайшлись би вершини (площі, перехрестя), між якими неможливо було б проїхати по місту без порушення правил дорожнього руху.

Розділимість. Зв’язний граф може бути розділено на незв’язні підграфи шляхом вилучення з нього деяких вершин та ребер. При вилученні вершин виключаються всі інцидентні їм ребра, а при вилученні ребер вершини зберігаються. Якщо існує така вершина, вилучення якої перетворює зв’язний граф у незв’язний, то вона називається точкою співчленіння, а ребро з такими властивостями називається містком (рис. 8.8)

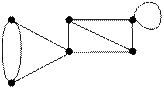
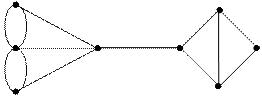
точка співчленення місток

Рис. 8.8 Графи з ознаками розділимості

Аналіз транспортної мережі на наявність точок співчленіння або містків проводиться з метою виявлення об’єктів, що потребують підвищеної охорони, бо їх руйнування призводить до розділення транспортної мережі, яка має стратегічне значення.

Дерева та ліс у графах. Графом типа «дерево» називається зв’язний ациклічний граф, наприклад, зображений на рис. 8.9.

Рис. 8.9 Граф – дерево

У дереві на множині р вершин завжди число ребер 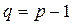, тобто мінімальна кількість, необхідна для того, щоби граф був зв’язаним.

При додаванні у дерево хоча б одного ребра утворюється цикл, а при видаленні – дерево розпадається на компоненти.

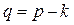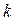Ліс – це незв’язний граф, компонентами якого є дерева. Очевидно, що в лісі число ребер , де - число дерев.

На певній кількості вершин може бути побудовано декілька істотно різних дерев, тобто таких, що не є ізоморфними. Наприклад, на рис.8.10 наведені всі можливі істотно різні дерева на шістьох вершинах.

послідовне дерево зіркове дерево

Рис. 8.10 Істотно різні (неізоморфні) дерева на шістьох вершинах.

Загальна ж кількість можливих дерев 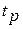, яка може бути побудована на множині вершин визначається за формулою

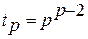. (8.1)

Орієнтоване дерево з коренем υ₀, для якого існує шлях з υ₀ в будь-яку іншу вершину, називається прадеревом (рис. 8.11). Такий граф відповідає структурі ієрархічної системи управління.

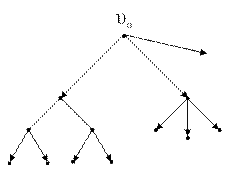
Рис. 8.11. Прадерево з коренем υ₀