Прикладні задачі теорії графів для транспортних систем
Найбільш розповсюдженими прикладами використання теорії графів у сфері створення та експлуатації транспортних систем є:
- формування раціональної структури транспортного обслуговування держави, регіону або міста (докладно розглядається в [1,16 ]);
- граф станів вагона та локомотива робочого парку, наприклад [ 19];
- визначення тарифної відстані у роботі підрозділів служби маркетингу та комерційної роботи;
- граф станційних маршрутів;
- критичний шлях при використанні сітьових графіків тощо.
9 Потоки в мережах
9.1 Загальні поняття
Граф, елементам якого поставлені у відповідність деякі параметри, називають зваженим графом або мережею. Параметри можуть бути задані на таких елементах, як вершини, дуги, підмножини вершин і дуг.
Розрізняють транспортні, інформаційні, електричні, гідравлічні мережі. Для характеристики мереж застосовується деякі поняття – функції на вершинах і дугах. Кожна вершина i характеризується інтенсивністю d (i). Вершини, для яких d (i)>0, називаються джерелами, а на яких d (i)<0 – стоками, інші вершини нейтральні, тобто на транспортній мережі джерела - станції навантаження (відправники), стоки – станції вивантаження (одержувачі). Для характеристики дуг введемо функцію пропускної спроможності, що ставить у відповідність кожній дузі (i, j) 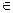 U графа G (I, U) ненегативне ціле число τ (i, j), називане пропускною спроможністю дуги. Для транспортних мереж це максимальна кількість вантажу, яку відповідна комунікація може пропустити за одиницю часу, тобто в мережі G (I,U) з одним джерелом S і одним стоком t задана функція пропускної спроможності τ (i, j), те в ній може бути задана також функція називана потоком.
U графа G (I, U) ненегативне ціле число τ (i, j), називане пропускною спроможністю дуги. Для транспортних мереж це максимальна кількість вантажу, яку відповідна комунікація може пропустити за одиницю часу, тобто в мережі G (I,U) з одним джерелом S і одним стоком t задана функція пропускної спроможності τ (i, j), те в ній може бути задана також функція називана потоком.
9.2 Задача про максимальний транспортний потік
Потоком у мережі називається функція, що зіставляє з кожною дугою (i, j) ціле число x (i, j) і має властивості:
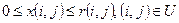 (9.1)
(9.1)
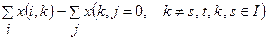 (9.2)
(9.2)
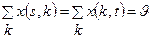 (9.3)
(9.3)
Для мережі потік x (i, j) по дузі (i, j) – це кількість тонн вантажу, що проходить через цю дугу в одиницю часу. Потоком у мережі називається сукупність {x (і, j)} потоків по всіх дугах мережі. Умова перша означає, що потік по кожній дузі ≥0 (ненегативний) і не перевищує пропускної спроможності дуги, (τ) – що кількість вантажу, що протікає в будь-яку нейтральну вершину мережі, дорівнює кількості вантажу, що випливає з її, тобто загальна кількість вантажу, що випливає зі стоку S дорівнює загальній кількості вантажу, що притікає в стік t (умова 3).
Лінійна її форма – величина потоку в мережі.
Розріз Розглянемо мережу G (I,U) з одним джерелом S і одним стоком t.
Якщо розбити безліч усіх вершин мережі G на дві непересічних підмножини R і R, то розрізом мережі, що відокремлює S від t називається сукупність усіх дуг (R, R), де S 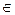 R, а t
R, а t 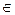 R.
R.
Тобто розріз складають усі ті і тільки ті дуги, що виходять з вершин і 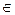 R і закінчуються у вершинах j
R і закінчуються у вершинах j 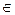 R.
R.
Сума пропускних спроможностей дуг розрізу складають пропускну спроможність (R, 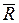 ) розрізу, тобто
) розрізу, тобто
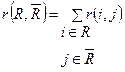 (9.4)
(9.4)
Розріз мережі, який має найменшу пропускну спроможність називається мінімальним розрізом.
 Приклад. Розглянемо мережу, наведену на рис.9.1
Приклад. Розглянемо мережу, наведену на рис.9.1
Рис. 9.1 Граф мережі з одним витіком s та одним стоком t.
Для цієї мережі існує 7 розрізів. Наприклад: 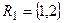 тоді
тоді 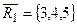 розріз
розріз 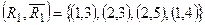 .
.
Пропускна спроможність 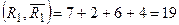 .
.
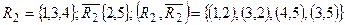
Пропускна спроможність 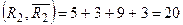 .
.
Мінімальний розріз 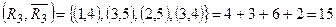
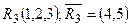
Властивість розрізу: розглядаємо довільний розріз (R, 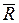 ). Який би шлях з S у t ми не розглядали, хоча б одна його дуга входить у даний розріз (R,
). Який би шлях з S у t ми не розглядали, хоча б одна його дуга входить у даний розріз (R, 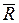 ), тому що S і t належать різним множинам R і
), тому що S і t належать різним множинам R і 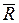 . Тобто якщо видалити всі дуги якого або розрізу, то в мережі не залишиться шляху, що веде з S до t, тобто будь-який розріз блокує всі шляхи з S у t. В зв’язку з тим що результат пропускної спроможності колій не може бути вище пропускної спроможності будь-якої його дуги, тому сумарний потік V, що тече з S у t по всіх можливих коліям, не може бути вище пропускної спроможності будь-якого розрізу мережі.
. Тобто якщо видалити всі дуги якого або розрізу, то в мережі не залишиться шляху, що веде з S до t, тобто будь-який розріз блокує всі шляхи з S у t. В зв’язку з тим що результат пропускної спроможності колій не може бути вище пропускної спроможності будь-якої його дуги, тому сумарний потік V, що тече з S у t по всіх можливих коліям, не може бути вище пропускної спроможності будь-якого розрізу мережі.
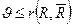 (9.5)
(9.5)
Тобто якщо знайти такий потік X*(і, j), що його величина V* дорівнює пропускної спроможності деякого розрізу 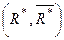
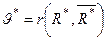 , то цей потік буде максимальним, а
, то цей потік буде максимальним, а 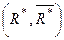 – розріз з мінімальною пропускною спроможністю.
– розріз з мінімальною пропускною спроможністю.
9.3 Теорема про максимальний потік і мінімальний розріз теорема (Форда – Фолкерсона)
Для будь-якої мережі з одним джерелом S і одним стоком t максимальна величина потоку з S у t дорівнює пропускної спроможності мінімального розрізу що відокремлює S від t. Розглянемо алгоритм рішення задачі про максимальний потік, є рішення в табличній формі.
За допомогою теорії про потоки в мережах зважуються задачі про оптимальний потік. У цьому випадку на ряду з пропускною спроможністю існує середня обумовлена на всіх дугах ,наприклад вартість.
У такій постановці розв'язується транспортна задача: у мережі G (I, U) існує функція x (i, j) 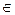 U така, що
U така, що
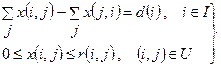 (9.6)
(9.6)
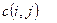 визначена на
визначена на 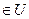
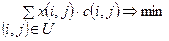 (9.7)
(9.7)
Потік x (i, j), задовольняючий умовам називається оптимальним. У матричній постановці всі пункти 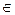 I, поділяються на дві категорії: відправлення і призначення, що зв'язані єдиним маршрутом, а пункти однієї категорії не зв'язані між собою. Однак у реальних задачах, крім пунктів виробництва і споживання є перевалочні пункти, не виробляючі і не споживаючі потік, аi сортувальна станція наприклад може бути зв'язана декількома маршрутами, що проходять через різні пункти мережі.
I, поділяються на дві категорії: відправлення і призначення, що зв'язані єдиним маршрутом, а пункти однієї категорії не зв'язані між собою. Однак у реальних задачах, крім пунктів виробництва і споживання є перевалочні пункти, не виробляючі і не споживаючі потік, аi сортувальна станція наприклад може бути зв'язана декількома маршрутами, що проходять через різні пункти мережі.
Дата добавления: 2015-03-07; просмотров: 1515;
