Суміжність у графах

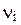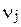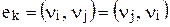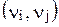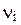Дві вершини та називаються суміжними, якщо вони є граничними вершинами ребра e_k. Відношення суміжності на множині вершин графа дозволяє представити кожне ребро як пару суміжних вершин: для неорієнтованих графів – неупорядковану, тобто ; для орграфів – упорядковану , де та 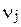- відповідно початкова та кінцева вершина дуги e_k.

Якщо граф заданий множиною вершин V та відношенням суміжності між ними, то граф може бути повністю представленим матрицею суміжності.

Матриця суміжності – це квадратна матриця розміром 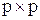, де р – число вершин графа. Кожний 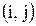елемент матриці дорівнює числу кратних ребер, з’єднуючих вершини 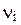та 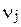, а для орграфа – числу суворо паралельних дуг, направлених від вершини 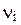до вершини .

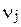Для графів(рис. 8.3 та 8.4, а) отримано матриці суміжності, що представлено відповідно на рис. 8.5

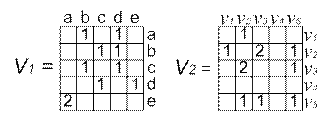
Рис. 8.5. Матриці суміжності графів

Для орієнтованого графа рядок відповідає початковій вершині дуги.

Для неорієнтованого графа матриця суміжності завжди симетрична відносно головної діагоналі, а для орграфу в загальному випадку – несиметрична. При цьому кожному ребру відповідає пара ненульових елементів, симетричних відносно головної діагоналі, дузі – ненульовий елемент матриці, петлі – ненульовий елемент головної діагоналі, ізольованій вершині – порожній рядок та порожній стовпець. Для зваженого графа без кратних ребер 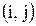- й елемент матриці суміжності дорівнює вазі дуги або ребра.

Матриця суміжності повністю (однозначно) визначає граф без петель та кратних ребер. Матриця суміжності зваженого графу, в якому вага ребер дорівнює інтенсивності поїздопотоків, представляє відому «шахматку», що використовується при плануванні експлуатаційної роботи залізничного підрозділу.