Типи графів

Орієнтовані графи. Часто зв’язки між деякими об’єктами (вершинами) характеризуються певно визначеною орієнтацією, наприклад, вулиці з однобічним рухом, підпорядкованість між рівнями управління та ін.. У такому випадку використовується ребро зі стрілкою, яке називається дугою (рис. 8.3а), а такий граф називається орієнтованим графом (орграфом)

а) б)

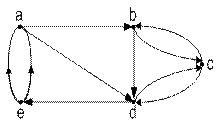
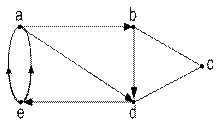
Рис. 8.3. Орієнтований граф (а) та змішаний граф (б).

Якщо між сусідніми вершинами є дві дуги або більше, то вони називаються паралельними (кратними). Коли дві дуги при вершині мають однаковий напрямок то їх називають суворо паралельними, а якщо протилежний напрямок – несуворо паралельними.

Несуворо паралельні дуги рівноцінні неорієнтованому ребру. Виконавши таку заміну, з орграфу отримаємо змішаний граф (рис. 8.3.б). І навпаки будь-який неорієнтований або змішаний граф можна перетворити в орграф заміною ребер несуворо паралельною парою дуг.

Таким чином, неорієнтований граф можна вважати частковим випадком орграфа. Неорієнтовані графи ще називаються співвіднесеними.

Зважені графи. Якщо кожному ребру або дузі приписати деяку кількісну або якісну характеристику його значимості (вагу) у порівнянні з іншими, то утвориться зважений граф. Вага ребра або дуги може означати, наприклад, довжину або пропускну спроможність шляхів сполучень, характер відносин між людьми, порядковий номер ребра та т.і.

Вагу можна приписати також і вершинам, наприклад, для транспортної системи це може бути потужність джерела, пропускна спроможність станції, чисельність мешканців населеного пункту, кількість колій у залізничному парку.

Кінцеві графи та їх різновиди. Якщо множина вершин графа кінцева, то такий граф називається кінцевим.

Кінцевий граф 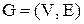, що містить р вершин та q ребер називається (р, q) – графом.

Розглянемо кінцевий (5, 6) – граф, що визначається множиною вершин 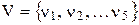та множиною ребер 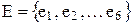(рис. 8.4, а)

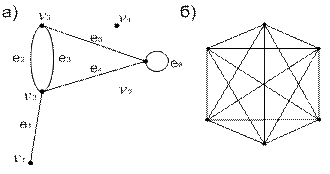
Рис. 8.4. Деякі типи кінцевих графів: а – псевдограф; б – повний 6-кутний граф.

В цьому графі ребра 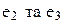є кратними. Ребро, граничними вершинами якого є одна й та ж вершина, називається петлею (е₆). В загальному випадку граф може містити й ізольовані вершини, що не зв’язані з іншими вершинами, наприклад v₄.

Визначення. Ступенем вершини графа 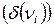називається кількість ребер, зв’язаних з даною вершиною ( петля враховується двічі). Для графа (рис. 8.4, а): 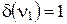, вершина 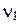називається кінцевою або висячою; ; .

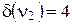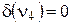Для орграфа розрізнюють позитивний ступінь 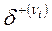– число дуг, що виходять з вершин, та негативний ступінь – число дуг, що входять у вершину. Для графа (рис. 8.3): ; .

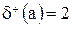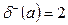Теорема 1. Сума ступенів всіх вершин будь-якого графа дорівнює подвійному числу ребер, а число вершин непарного ступеню завжди є парним.

Теорема 2. В орграфі суми всіх позитивних і негативних ступенів вершин є рівними між собою та дорівнюють числу всіх дуг.

Основні різновиди кінцевих графів:

1) граф без петель та кратних ребер називається простим (звичайним ) наприклад рис. 8.1;

2) граф без петель, але з кратними ребрами називається мультиграфом (рис. 8.2);

3) найбільш загальний вид граф з петлями та кратними ребрами називається псевдографом (рис. 8.4, а);

4) граф, всі вершини якого з’єднані ребрами між собою, називається повним (рис. 8.4, б);

5) граф, у якого є вершини, але немає ребер, тобто всі вершини ізольовані, називається пустим або нуль-графом.