Проницаемость зависит от направления - имеет место обобщенный закон Дарси

,

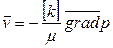(2.39)

где 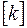– тензор проницаемости.

Если воспользоваться системой координат, оси которой совпадают с главными осями тензора 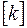, то уравнение (2.39) в проекциях на оси декартовой системы координат перепишется в виде

,

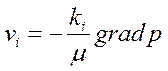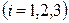(2.40)

где 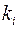– проницаемости вдоль главных осей 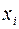анизотропии. При этом проекция скорости фильтрации на нормаль к элементарной площадке вычисляется по формуле

.

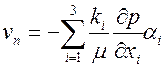(2.41)

Подставляя (2.40) в (2.32) получим уравнение при установившейся фильтрации

.

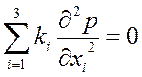(2.42)

Учитывая (2.41), усложняются и граничные условия вида (2.37) и (2.38).

Однако граничную задачу, связанную с уравнением (2.42), легко свести к граничной задаче, связанной с уравнением Лапласа (2.34), если вести следующую замену переменных:

для пространства

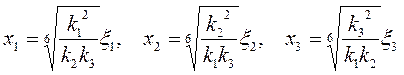
для плоскости

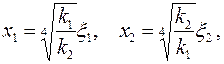
(2.43)

где 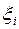– новые координаты.

Это означает геометрическое преобразование анизотропной области 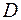в некоторую изотропную область 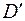, проницаемость которой

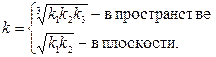
(2.44)

При этом граница 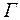области 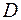преобразуется в границу 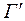области 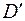. Например, область, ограниченная окружностью

,

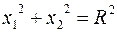(2.45)

преобразуется согласно (2.42) в область, ограниченную эллипсом

.

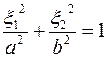(2.46)

или в параметрическом виде

.

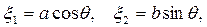где 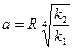, 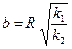- полуоси элипса