УРАВНЕНИЯ СОСТОЯНИЯ

Уравнения неразрывности и движения (2.3) и (2.9), справедли­вые при непрерывных движениях любой сплошной среды, недоста­точны для описания поведения конкретной среды, так как их число меньше числа входящих в них неизвестных (перемещения, дефор­мации, скорости, напряжения и др.). Это понятно и с другой точки зрения. Различные реальные тела при одних и тех же внешних усло­виях ведут себя по-разному, что никак не отражено в общих уравне­ниях (2.3) и (2.9). Поэтому говорят, что такая система уравнений не замкнута. Построить замкнутую систему уравнений — значит построить математическую модель изучаемой сплошной среды. Для этого к имеющимся уравнениям необходимо присоединить так называемые механические уравнения состояния, которые выра­жают связь между кинематическими и динамическими величинами.

Механические свойства реальных тел довольно сложны, и поэтому уравнения состояния устанавливаются на основании опытных данных. В настоящее время для многих тел установлены определенные механические свойства и соответствующие им уравнения состояния.

В силу характерных особенностей различают математические модели твердых деформируемых тел, жидкостей и газов, хотя такое деление в определенном смысле условно.

С позиций механики сплошной среды твердые тела, жидкости и газы различаются по действию, оказываемому на них внешними силами, именно по неодинаковой сопротивляемости изменению формы. Газы практически не сопротивляются изменению формы, капельные жидкости сопротивляются изменению формы значи­тельно слабее, чем твердые тела. Кроме того, они различаются по характеру и степени проявления упругих, вязких и пластических свойств, их влиянию на изучаемый процесс.

Все это находит отражение в уравнениях состояния, т. е. в зависимостях между компонентами тензоров напряжений σ_ij и деформаций ε_ij (или скорости деформаций ξ_ij) или компонентами девиаторов напряжений s_ij и деформации e_ij (или скорости деформаций λ_ij). По существу эти уравнения являются классифи­катором разделов механики сплошной среды.

При формулировке инженерных задач не следует стремиться к использованию уравнений состояния, описывающих все детали механического поведения тела под воздействием внешних сил. Наоборот, целесообразно выбрать простейшую математическую модель, которая отражала бы лишь самые существенные свойства. В противном случае решить задачу будет либо чрезвычайно сложно, либо вовсе невозможно.

Приведем наиболее известные уравне­ния состояния, используемые в гидромеханике и механике твердо­го деформируемого тела.

Следует обратить внимание, что структурное сходство этих моделей придает общность исходным уравнениям механики сплошной среды, несмотря на существенное различие в физиче­ском поведении разных тел.

§ 4. УРАВНЕНИЯ СОСТОЯНИЯ ГИДРОМЕХАНИКИ

1. Модель идеальной жидкости– это простейшая механическая модель сплошной среды, для которой характерно отсутст­вие сопротивления (сил трения) при скольжении одного слоя жидкости по другому, отдельные части взаимодействуют только в виде нормального давления, т. е. в любой точке идеальной жидкости касательные напряжения

,

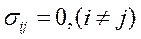а нормальные напряжения

,

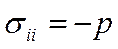или через компоненты девиатора напряжений

.

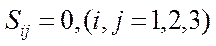Уравнением состояния для этой жидкости служит зависимость плотности ρ от давления р и температуры Т:

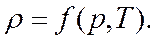(2.11)