В декартовой системе координат
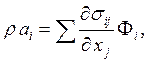(i=1,2,3)
где проекции ускорения ai вычисляют по формулам (1.6).
Эти уравнения, связывающие компоненты vi вектора скорости и тензора напряжений {σij}, являются основной системой дифференциальных уравнений движения для любой сплошной среды, представляющих собой уравнение баланса количества движения (или импульса) для бесконечно малого объема среды.
Если движения частиц происходят без ускорения (ai=0) или они пренебрежимо малы, то уравнения (2.9) называются дифференциальными уравнениями равновесия.
При непрерывном движении сплошной среды теорема моментов количества движения (2.7) в дифференциальной форме сводится к выводу о том, что тензор напряжений симметричен, т. е. σij = σji.Если тензор напряжений симметричен, то уравнения моментов количества движения удовлетворяются тождественно.
Интегральная теорема живых сил (2.8) эквивалентна следующему дифференциальному уравнению:
dТ = dЕ = dA(e) (2.10)
где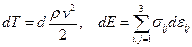 
— соответственно изменение кинетической и потенциальной энергии бесконечно малого объема сплошной среды;
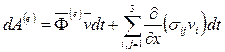— элементарная работа внешних объемных и поверхностных сил, действующих на бесконечно малый элемент объема среды.
Уравнение (2.10) является следствием уравнений движения (2.9) и представляет собой уравнение баланса механической энергии. В общем случае оно не является законом сохранения энергии, но его можно так трактовать тогда, когда механическая энергия тела не переходит в тепловую или другие виды энергии. Общий закон сохранения энергии в этом случае распадается на два: закон сохранения механической энергии и закон сохранения энергии другого вида.
Дата добавления: 2015-03-07; просмотров: 947;