Одно из наиболее известных уравнений движения идеальной жидкости — закон Бернулли
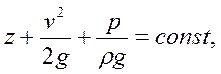
который гласит, что при установившемся движении несжимаемой идеальной жидкости сумма геометрической (z),скоростной (v2/2g) и пьезометрической (p/ρg) высот вдоль линии тока остается величиной постоянной.
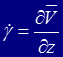 2. Модель - вязкой ньютоновской жидкости - следующая по сложности, которую используют, когда силами трения или напряжениями сдвиги при движении жидкости пренебречь нельзя, Уравнениями состояния для такой жидкости, кроме уравнения вида (2.11),
2. Модель - вязкой ньютоновской жидкости - следующая по сложности, которую используют, когда силами трения или напряжениями сдвиги при движении жидкости пренебречь нельзя, Уравнениями состояния для такой жидкости, кроме уравнения вида (2.11), 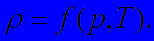
будет
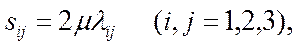 (2.12)
(2.12)
т.е. прямо пропорциональная зависимость между компонентами девиатора напряжений и скоростей деформаций.Учитывая динамические величины и элементы теории напряжений, имеем равносильные уравнения, выраженные через компоненты тензоров напряжений и скоростей деформаций:
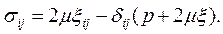
При плоском слоистом течении жидкости вдоль оси Оx1, когда v1 =v1(x1, х2), v2 = v3 = 0, нормальные и касательные напряжения равны:
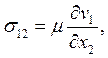
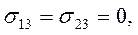
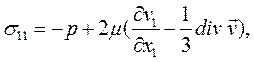
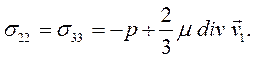
Если, кроме того, жидкость несжимаемая 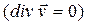 и скорость v1 не зависит от х1, то уравнение состояния имеет простейший вид
и скорость v1 не зависит от х1, то уравнение состояния имеет простейший вид
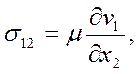
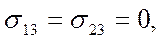
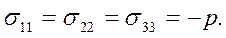
Коэффициент пропорциональности μ называется коэффициентом вязкости или динамической вязкостью жидкости. Размерность этого коэффициента, согласно соотношениям (2.12), будет 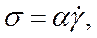
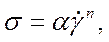
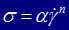

Дата добавления: 2015-03-07; просмотров: 912;
