Для модели Шведова — Бингама

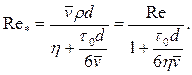(2.19)

Нижняя граница критических значений обобщенных парамет­ров Rе', Rе_* равна 2100.

Наряду с изучением переходных процессов в цилиндрических трубах были изучены движение жидкостей в пространстве между соосными цилиндрами в осевом и тангенциальном направлениях и при обтекании твердых тел набегающим потоком жидкости, а также обнаружено качественное сходство переходных процессов, определя­емых по тем же параметрам Рейнольдса (2.18) и (2.19), где под d следует понимать характерное сечение потока или линейный размер тел.

Изучение переходных режимов и практическое определение Rе базируются главным образом на установлении опытной зависимости коэффициента гидравлического сопротивления от параметра Рей­нольдса, соответствующего данной реологической модели.

Отличительным признаком турбулентных течений является зависимость скорости от времени в любой точке потока. Для количественного описания турбулентных течений О. Рейнольдc предложилдействительные скорости потока v_i (i = 1, 2, 3) в данной точке представлять в виде суммы средних во времени скоростей 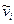и пульсационных скоростей (пульсаций) 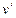, т. е. 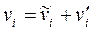. Анало­гично представляется и давление 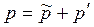. Форма уравнений движения и неразрывности сохра­няется. В этом случае следует только заменить скорости v_i и давление р средними скоростями 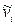и давлениями 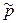, а вместо напряжений 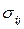использовать сумму

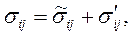
где 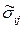— компоненты напряжений, связанные со средними ско­ростями уравнениями состояния (2.12), (2.15) или (2.16); 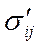— допол­нительные компоненты напряжений, возникающие вследствие пульсаций, они называются напряжениями Рейнольдса.

Иначе говоря, доказана возможность применения основных уравнений движения механики сплошной среды для решения задач турбулентного течения при условии, что величины v_i, р и 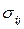, входящие в эти уравнения, заменены соответственно на величины 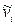, 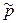и .

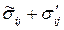Предложено несколько полуэмпирических уравнений состояния для напряжений Рейнольдса 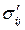. Наиболее известно и широко используется уравнение Прандтля:

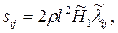(2.20)

где l —коэффициент, характеризующий геометрическую структуру турбулентного потока, называемый путем смешения (перемешивания) или масштабом турбулентности, зависящий от расстояния до стенки канала.

В частном случае при течении жидкости между параллельными плоскостями в направлении оси Ох₁ уравнение (2.20) принимает вид

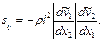
Прандтль, анализируя свойства турбулентного потока в трубах вблизи твердой стенки, принимал l = 0,36s, где s — расстояние от стенки трубы.

6. Модель неньютоновских многокомпонентных смесей вязкопластичных жидкостей при любых режимах течения. Таким образом, общая задача гидромеханики в определении компонент v_i (i = 1, 2, 3) вектора скорости 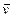, компонент симметричного девиатора напряжений s_ij =s_ji (i, j=1, 2, 3), давления р и плотности ρ жидкости в любой точке области.

В общем случае эти одиннадцать искомых функций должны в ламинарном режиме течения удовлетворять следующей системе дифференциальных уравнений: