И механического состояния

s = f(p); (2.23)

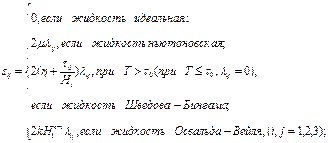(2.24)

Подставляя в уравнения (2.21) соотношения (2.24)можно получить уравнения Навье — Стокса, Генки — Ильюшина и др.

При турбулентных течениях жидкостей и газов, согласно сказанному выше, система уравнений (2.21) — (2.24) сохраняет свой вид, но под величинами v_i, 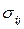, р необходимо понимать усреднен­ные по времени значения 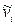, , 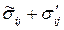, 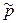где напряжения Рейнольдса 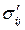связаны с компонентами средних скоростей деформаций 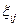, например, уравнением Прандтля (2.20).

Для удобства выпишем обозначения основных величин:

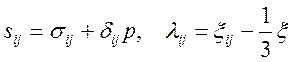- компоненты девиаторов напряжений и скоростей деформаций соответственно;

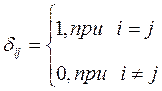- символ Кронекера;

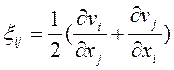—соотношения Коши;(2.25)

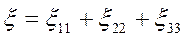— скорость деформации объема;

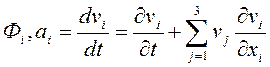— проекции объемных сил и ускорении;

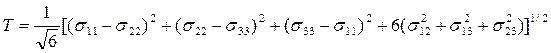-(2.26)

интенсивность касательных напряжении;

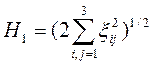- (2.27)

интенсивность скорости деформации сдвига при ξ=0.

Единственность и однозначность решения системы дифференциальных уравнений (2.21) - (2.24) возможны лишь при выполнении граничных условий:

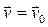— на поверхности контакта жидкость - твердое тело и (или) p=p₀ - на свободной поверхности, где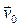

Лекция 3. ЗАДАЧИ ФИЛЬТРАЦИИ ПРИ СТРОИТЕЛЬСТВЕ СКВАЖИН

§ 1.ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ ФИЛЬТРАЦИИ.

В этих трёх лекциях приведены основные положения теории фильтрации одномерных потоков однородных и неоднородных жидкостей и газов при установившихся и неустановившихся процессах. Большое внимание уделено пространственным задачам теории фильтрации жидкостей и газов и их смесей при установившихся и нестационарных изотермических процессах. Дано развитие теории притока сжимаемой жидкости и газа к несовершенным скважинам при линейном и нелинейном законах фильтрации, методам расчета добавочных фильтрационных сопротивлений. Изложены основные положения теории фильтрации в двойных средах. Рассмотрены задачи притока к трещинам гидравлического разрыва пласта и горизонтальным стволам, особенности фильтрации жидкости и газа в деформируемом пласте. Изложена теория вытеснения одной жидкости другой, фильтрация газоконденсатных смесей, теория конусообразования и соответствующие им прикладные задачи.

Изложенные положения базируются на современных достижениях науки и практики в теории фильтрации и разработки нефтяных, нефтегазовых и газоконденсатных месторождений, науки о движении жидкостей, газов и их смесей в пористых и трещиноватых горных породах. Она является об­ластью гидромеханики, в которой рассматривается не движение жидкостей и газов вообще, а особый вид их движения — фильтрация, которая имеет свои специфические особенности. Она служит теоретической основой раз­работки нефтяных, газовых и газоконденсатных месторождений. Методами теории фильтрации решаются важнейшие задачи гидрогео­логии, расчет притоков жидкости к искусственным водозаборам и дренажным со­оружениям, изучение режимов естественных источников и подземных по­токов, расчет фильтрации воды в связи с сооружением и эксплуатацией плотин, понижением уровня грунтовых вод, задачи о движении реагентов через пористые среды и специ­альные фильтры, фильтрация жидкостей и газов через стенки пористых со­судов и труб — вот далеко не полный перечень областей широкого ис­пользования методов теории фильтрации.

Начало развитию подземной гидромеханики было положено фран­цузским инженером Анри Дарси (1803-1858 гг.), который в процессе работы над проектом водоснабжения г. Дижона (Франция) провел многочислен­ные опыты по изучению фильтрации воды через вертикальные песчаные фильтры. В опубликованной в 1856 г. замечательной книге А. Дарси дал подробное описание своих опытов и сформулировал обнаруженный им экспериментальный закон, в соответствии с которым скорость фильтрации жидкости прямо пропорциональна градиенту давления.

Закон Дарси (Анри Дарси, 1856) — закон фильтрации жидкостей и газов в пористой среде. Исторически закон был получен А.Дарси экспериментально, но может быть получен с помощью осреднения уравнений Навье – Стокса, описывающих течение в масштабе пор (в настоящее время имеются доказательства для пористых сред с периодической и случайной микроструктурой). Выражает зависимость скорости фильтрации флюида от градиента напора:

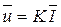
где: 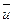— скорость фильтрации, 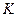— коэффициент фильтрации, 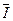— градиент напора.

Анри Филибер Гаспар Дарси (фр. Henry Philibert Gaspard Darcy, 10 июня 1803, Дижон, — 2 января 1858, Париж) — французский инженер-гидравлик, обосновавший закон Дарси (1856), связывающий скорость фильтрации жидкости в пористой среде с градиентом давления: «По-видимому, для песка одного качества, пропускаемый им расход прямо пропорционален напору и обратно пропорционален толщине фильтрующего слоя (грунта)».

Именем Дарси названа единица измерения проницаемости пористой среды.

Под руководством Дарси в г. Дижоне была создана первая в Европе система городских очистных сооружений с различными фильтрационными засыпками. Это настолько изменило город в лучшую сторону, что уже на следующий день после смерти Дарси от пневмонии главной площади города было присвоено его имя.

В эти же годы другой французский инженер Жюль Дюпюи (1804- 1866 гг.) опубликовал монографию, в которой впервые изложил гидрав­лическую теорию движения грунтовых вод, вывел формулы для расчета дебитов колодцев и дрен, названные его именем, решил другие фильтра­ционные задачи.