Непрерывные цепи Маркова.

Случайный процесс X(t) с дискретным множеством значений образует непрерывную цепь Маркова, если

.

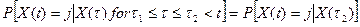Будущие состояния зависят от прошлого только через текущее состояние. Для непрерывный цепей Маркова основным также является уравнение Чепмена –Колмогорова, для однородной цепи имеющее вид: .

Здесь матрица H(t)= [ p_ij(t)] - матрица вероятностей перехода из состояния i в состояние j в момент времени t , а матрица Q называется матрицей интенсивностей переходов. Ее элементы имеют следующий смысл: если в момент времени t система находилась в состоянии E_i , то вероятность перехода в течение промежутка времени (t,t+Δt) в произвольное состояние E_j задается величиной q_ij(t)Δt + o(Δt), а вероятность ухода из состояния E_i величиной -q_iiΔt + o(Δt).

Таким образом, интенсивности переходов можно вычислять как соответствующие пределы при стремлении к нулю длительности временного интервала.

Наиболее важным для дальнейшего использования является класс непрерывных цепей Маркова называемых «процессами гибели - размножения»(Birth – death process). Для таких систем из состояния k возможны переходы только в состояния k, k-1 и k+1 в следующие моменты времени:

· в момент t объем популяции был равен k и в течение времени (t,t+Δt) не произошло изменения состояния

· в момент t объем популяции был равен k-1 и в течение времени (t,t+Δt) родился один член популяции

· в момент времени t объем популяции был равен k+1 и в течение времени (t,t+Δt) погиб один член популяции

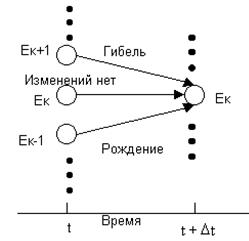
Рис. 2 Возможные переходы в состояние Ек.

Диаграмма переходов для дискретных цепей Маркова (Рис 3)

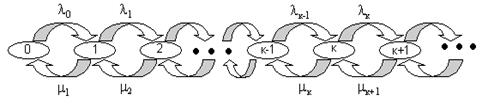
Рис.3 Диаграмма интенсивностей переходов для процесса размножения и гибели.

Овалам здесь соответствуют дискретные состояния, а стрелки определяют интенсивности потоков вероятности (а не вероятности!) переходов от одного состояния к другому.

Имеет место своеобразный «закон сохранения»:

Разность между суммой интенсивностей, с которой система попадает в состояние k и суммой интенсивностей, с которой система покидает это состояние должна равняться интенсивности изменения потока в это состояние (производной по времени).

Применение закона сохранения позволяет получать уравнения для любой подсистемы Марковской цепи типа процесса «гибели-размножения». Особенно эффективным оказывается построение решений в стационарном, установившемся режиме, когда можно полагать что вероятности в произвольный, достаточно отдаленный момент времени, остаются постоянными.

Система М/M/1. Анализ.

Это система с пуассоновским входным потоком заявок, экспоненциальным законом распределения времени обслуживания и одним сервером.

На рис. 1. приведена простейшая схема такой системы. Она содержит буфер, который может хранить очередь бесконечной длины, состояние которой может быть отождествлено с числом заявок, содержащихся в очереди в каждый момент времени.

Рис. 1. СМО типа М/М/1.

Поскольку входной процесс ординарный, то в каждый момент времени к очереди может добавиться только одна заявка, поскольку сервер один, то в каждый момент времени может быть обслужена, то есть уйти из очереди только одна заявка. Таким образом, рассматриваемая СМО относится к процессу класса «гибели-размножения». Для анализа необходимо конкретизировать параметры системы. Распределение вероятностей входного потока и времени обслуживания позволяет полагать интенсивности вероятностей в модели постоянными.

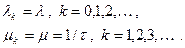
Здесь t – среднее время обслуживания в сервере.

На рис 2 приведена диаграмма интенсивностей переходов для рассматриваемой системы.

Рис. 2 Диаграмма интенсивности переходов для СМО типа М/М/1.

Полученное ранее общее решение позволяет сразу записать вероятность того, что в стационарном состоянии в очереди будет находиться k заявок

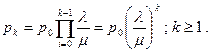
Найдем начальное значение вероятности, учитывая сходимость соответствующего ряда

.

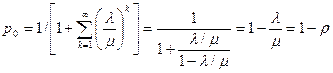Окончательно получаем формулу для вероятности длины очереди

.