Математическое введение в теорию цепей Маркова

Дискретные цепи Маркова.

Задана дискретная цепь Маркова, если для последовательности случайных величин выполняется равенство

.

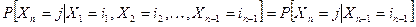Это означает, что поток случайных величин определяется только вероятностью перехода от предыдущего значения случайной величины к последующему. Зная начальное распределение вероятностей, можно найти распределение на любом шаге. Величины i_n можно интерпретировать как номера состояний некоторой динамической системы с дискретным множеством состояний. Если вероятности переходов не зависят от номера шага, то такая цепь Маркова называется однородной и ее определение задается набором вероятностей .

Для однородной Марковской цепи можно определить вероятности перехода из состояния i в состояние j за m шагов

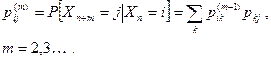
Цепь Маркова называется неприводимой, если каждое ее состояние может быть достигнуто из любого другого состояния. Состояние i называется поглощающим, если для него p_ii =1.

Состояние называется возвратным, если вероятность попадания в него за конечное число шагов равна единице. В другом случае состояние относится к невозвратным. Возвратное состояние может быть периодическими апериодическим в зависимости от наличия кратных шагов возврата. Введем вероятности возврата в состояние i через n шагов после ухода из этого состояния:

Они позволяют определить среднее число шагов, т.е среднее время возврата: .

Состояние называется возвратным нулевым, если среднее время возвращения в него равно бесконечности, и возвратным ненулевым, если это время конечно.

Теорема 1.

Состояния неприводимой цепи Маркова либо все невозвратные, либо все возвратные нулевые, либо все возвратные ненулевые. В случае периодической цепи все состояния имеют один и тот же период.

Вторая теорема рассматривает вероятности достижения состояний в стационарном (то есть не зависящем от начального распределения вероятностей) режиме.

Теорема 2.

Для неприводимой и апериодической цепи Маркова всегда существуют предельные вероятности, не зависящие от начального распределения вероятностей. Более того, имеет место одна из следующих двух возможностей:

А) все состояния цепи невозвратные или все возвратные нулевые, и тогда все предельные вероятности равны нулю и стационарного состояния не существует;

Б) все состояния возвратные ненулевые и тогда существует стационарное распределение вероятностей:

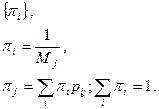
Состояние называется эргодическим, если оно апериодично и возвратно ненулевое. Если все состояния цепи Маркова эргодичны, то вся цепь называется эргодической. Предельные вероятности эргодической цепи Маркова называют вероятностями состояния равновесия, имея в виду, что зависимость от начального распределения вероятностей полностью отсутствует.

Цепь Маркова с конечным числом состояний (конечная цепь), удобно изображать в виде ориентированного графа, называемого диаграммой переходов (рис.1). Вершины графа ассоциируются с состояниями, а ребра с вероятностями переходов.

Вычисления вероятностей достижения состояний производится прямыми методами или с помощью z-преобразования.

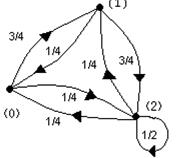
Рис. 1. Цепь Маркова.

У однородных Марковских процессов вероятности переходов не зависят от времени.

Вероятности перехода системы из состояния i на m-том шаге в состояние j на n-том шаге для n > m.

Эти вероятности связаны между собой, так называемым уравнениями Чепмена-Колмогорова.(Chapman - Kolmogorov)

.

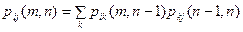Для однородных цепей Маркова эти уравнения упрощаются так

.