Измерение фазы выходного напряжения

Фазу выходного напряжения описанных преобразователей определяют относительно фазы опорного напряжения, за которое может быть принято напряжение любой статорной катушки, при этом нулевое положение ротора определяется совпадением магнитной оси обмотки ротора и той катушки, напряжение которой принято за опорное (рис.1).

Измерение фазы обычно производится фазометрами, которые бывают различных типов. Большую точность измерения фазы можно получить при использовании времяимпульсного метода преобразования, который заключается в получении импульсов с частотой питающего напряжения, но длительностью, пропорциональной фазе выходного напряжения. Указанный метод позволяет получить аналоговый или цифровой сигнал.

Последовательность преобразований опорного и выходного напряжений показана на (рис. 3).

Сдвиг фазы выходного напряжения j может быть легко определён сравнением наиболее характерных одноименных точек кривых (рис. 3а), например, нулевых моментов. Для этого синусоидальные напряжения преобразуют в прямоугольные той же частоты (рис. 3б), тогда время сдвига между прямоугольными импульсами:

, (2.2.7)

и изменяется в зависимости от изменения фазы в пределах периода сравниваемых напряжений – .

Для перехода от времени сдвига к импульсу прямоугольного напряжения с длительностью (рис.3 г) применяется статический триггер, который схематично изображен на рис.4.

Триггер является двоичным элементом памяти, т.е. имеет два устойчивых состояния (1 и 0) с двумя входами и и двумя выходами (прямой) и (инверсный). При подаче импульса напряжения на вход , т.е. на ‘1’, на выходах будут сохраняться соответственно – ‘1’ ( ) и ‘0’ ( ) до тех пор, пока не поступит ‘1’ на вход . При этом триггер занимает другое устойчивое состояние т.е. на выходах будут соответственно ‘0’ ( ) и ‘1’ ( ).

Процесс повторится при поступлении ‘1’ на вход .

Если на входы и подавать импульсы с одинаковой периодичностью, но сдвинутые по времени, то на выходах получим прямоугольные импульсы той же периодичности, но с разной шириной для равной времени сдвига – , а для дополнением до периода .

Следовательно, если продифференцировать прямоугольные напряжения и и подать импульсы, соответствующие производным их передних фронтов (рис. 3в), на входы и , тогда на выходе получим прямоугольный импульс , пропорционально разности фаз опорного и выходного напряжения, т.е. углу поворота ротора сельсина a. Проинтегрировав данный импульс за период при условии постоянства – , получим аналоговый сигнал, пропорциональный .

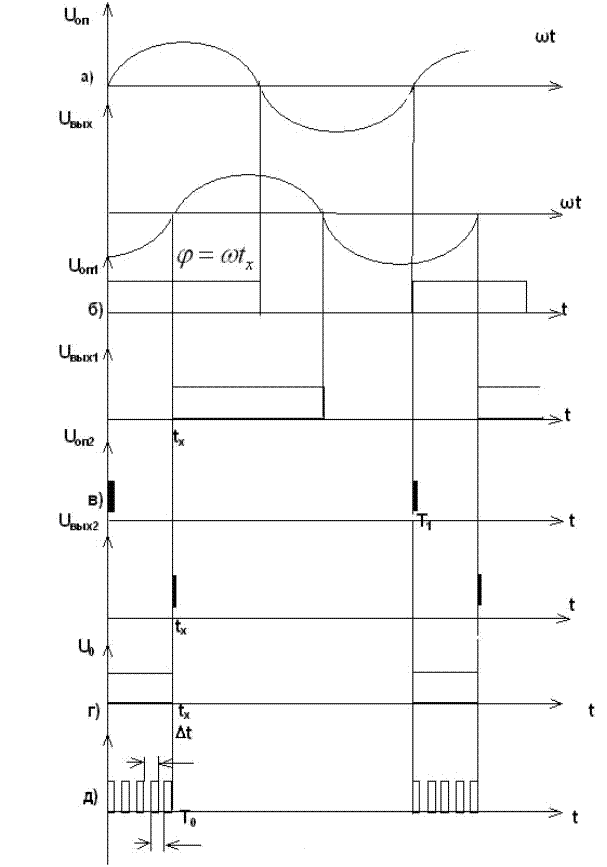
Рис. 3. Последовательность преобразования угла сдвига фаз

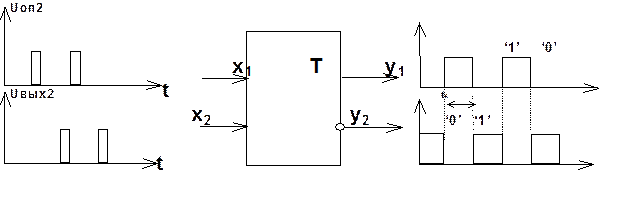Рис. 4. Схема работы триггера

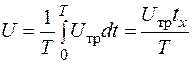(2.2.8)

Воспользовавшись уравнением (2.2.7), имеем:

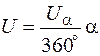(2.2.9)

Большую точность можно получить при цифровом методе измерения времени . Для перехода к цифровому методу необходимо преобразовать непрерывную (аналоговую) величину интервала времени в дискретную величину (рис.5) равную числу прошедших к счетчику импульсов (метод последовательного счета). В этом случае выходной величиной является количество импульсов , которое пропорционально времени .

, (2.2.10)

где – период следования квантующих импульсов.

Так как в общем случае в измеряемый интервал укладывается не целое число импульсов, то возникает погрешность от дискретности, которая носит методический характер. Тогда уравнение (2.2.10) можно записать в следующем виде:

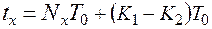(2.2.11)

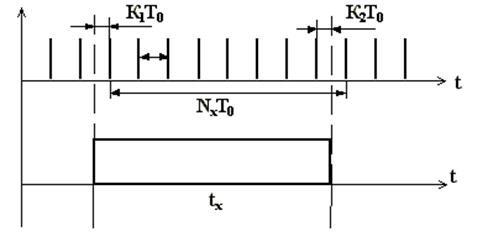
Рис. 5. Преобразование временного интервалы в импульсы

Таким образом, счетчик отсчитает целую часть , а дробная часть, в которой и могут принимать значения при или при и все значения между 0 и 1 является абсолютной погрешностью:

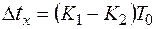(2.2.12)

Эта величина является случайной, а максимальное значение абсолютной погрешности счета, очевидно, равно 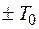(при , или при , ).

Уменьшить эту погрешность можно уменьшая период следования 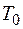, но здесь существует предел, накладываемый допустимой без ошибок скоростью счета современных счетчиков.

Для считывания в лабораторных условиях используется цифровой частотомер.

Если время измерения 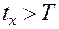, необходимо определить из выражения:

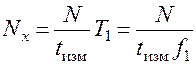(2.2.13)

где 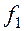– частота опорного напряжения;

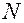– показания частотомера при времени измерения 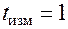сек, т.к. при измерении частоты независимо от выставленного времени измерения оно приводится к 1 с.

В процессе работы из-за нестабильност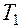и и 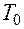, , 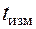а также из-за случайного характера величин и может получиться не целое число , в этом случае его необходимо округлить до ближайшего целого.

При максимальной абсолютной погрешности измерения времени импульса 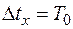можно определить погрешность измерения фазы (угла поворота) из уравнения (5.2.9), т.е. при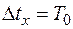

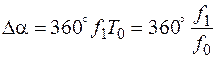(2.2.14)

где 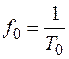– частота квантующего генератора.

Кроме рассмотренной методической погрешности от дискретности, суммарная погрешность определится следующими факторами:

а) неравенством амплитуд линейных напряжений;

б) изменением фазы между напряжениями;

в) не синусоидальностью питающих напряжений;

г) неточностью симметрирования обмоток;

д) технологическими.

Следовательно, у фазовых преобразователей суммарная погрешность зависит от многих факторов. При исследовании индукционного фазовращателя следует определить суммарную погрешность и выделить максимальную погрешность от дискретности.