Избыточные связи

Избыточными называют такие связи, которые не накладывают новых ограничений на перемещения звеньев механизма, а только повторяют уже существующие. Избыточные связи могут быть как в отдельных кинематических парах, так и на уровне механизма в целом. Различают избыточные связи трех типов: А, Б и В (по предложению профессора Озола).

Избыточные связи типа А имеют место в отдельных кинематических парах. Для передачи усилия от одного звена к другому теоретически достаточно контакта в одной точке (Рис. 10,а). Если передача усилия обеспечивается поверхностным контактом, то соприкосновение звеньев во всех точках поверхности, кроме одной, будет образовывать избыточные связи типа А (Рис. 10,б).

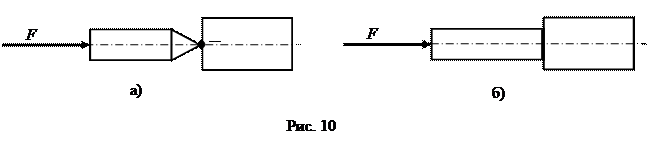
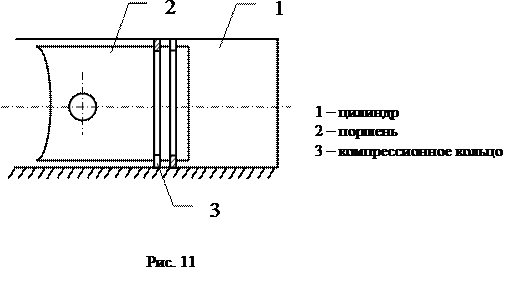
Избыточные связи типа А являются полезными, когда требуется передача значительных усилий, поскольку звенья реальных механизмов не являются абсолютно твердыми, и в случае точечного контакта при большой силовой нагрузке будут иметь место существенные деформации, возможно также разрушение звеньев в зоне их соприкосновения. В отдельных случаях связи типа А являются вредными и устраняются. Например, кинематическая пара цилиндр-поршень в двигателе внутреннего сгорания будет работоспособной, если поверхностный контакт поршня с цилиндром заменить линейным контактом цилиндра с компрессионными кольцами (Рис. 11).

Избыточные связи типа Б имеют место в кинематических парах с ветвлением. Число избыточных связей типа Б рассчитывается по формуле:

,

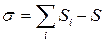где i - индекс ветвления пары, S_i – число независимых связей в i – той ветви, S – класс кинематической пары.

Пример

На рис. 12 изображена поступательная кинематическая пара с двумя ветвлениями.

Рассчитаем число избыточных связей типа Б: , 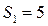(ветвление поступательное), 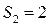(ветвление цилиндр-плоскость) 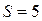(класс поступательной пары – пятый),

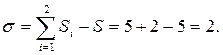
Избыточные связи типа Б увеличивают жесткость кинематической пары, но требуют повышенной точности изготовления звеньев и сборки пары.

Избыточные связи типа В образуются при замыкании кинематических цепей в контуры, отсюда их второе название – контурные избыточные связи. Их число определяется по формуле Озола:

,

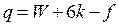где W – число степеней свободы механизма, k – число замкнутых кинематических контуров, f – суммарное число степеней свободы кинематических пар механизма. Для плоского механизма число контурных избыточных связей может быть также найдено по формуле Малышева:

,

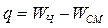где W_Ч – число степеней свободы механизма, рассчитанное по формуле Чебышева, W_СМ – число степеней свободы того же механизма, рассчитанное по формуле Сомова – Малышева.

Задача

Определить число избыточных связей в плоском шарнирном четырехзвенном механизме (Рис. 7,а).

Решение

Для данного механизма 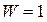, 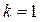(один замкнутый контур) и 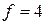(четыре одноподвижные кинематические пары). Тогда по формуле Озола:

.

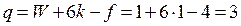Механизм имеет три контурные избыточные связи, что и было отмечено в Задаче 2 п. 1.6.

Контурные избыточные связи увеличивают жесткость механизма, но требуют повышенной точности изготовления звеньев и сборки механизма. При необходимости, они могут быть устранены путем понижения класса одной или нескольких кинематических пар.

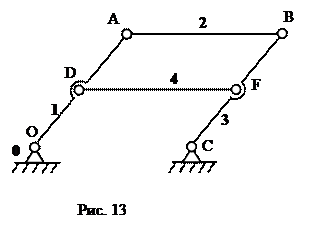
Избыточные связи могут быть также привнесены в механизм путем введения в его схему дополнительных звеньев. Рассмотрим механизм сдвоенного параллелограмма (рис. 13). Здесь дополнительное звено – шатун 4. Так как механизм плоский, рассчитаем его число степеней свободы по формуле Чебышева ( , ):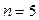

.

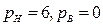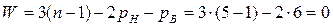Полученный результат означает, что с точки зрения структурного строения, рассматриваемая система механизмом не является. Для того чтобы возникла одна степень свободы, требуется соблюдение геометрических условий: 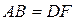, , 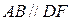, 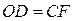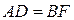. Следовательно, введение дополнительных звеньев в схему механизма влечет за собой необходимость точного соблюдения определенных геометрических размеров при изготовлении звеньев.