Местные подвижности

Местными подвижностями называются степени свободы механизма, не оказывающие влияния на передачу основного движения.

Рассмотрим механизм (Рис. 9). По формуле Сомова – Малышева число его степеней свободы ( , , )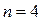

.

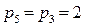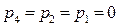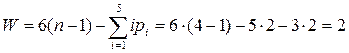То есть, этот механизм не только существует как пространственный, но еще имеет две степени свободы. Одна степень свободы здесь является основной подвижностью, необходимой для передачи движения от звена 1 к звену 3. Вторая степень свободы (вращение шатуна 2 вокруг собственной оси) не влияет на передачу основного движения, поэтому является местной подвижностью.

В общем случае, механизм может иметь как основные, так и местные подвижности: его число степеней свободы определяется равенством:

,

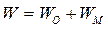где W_O – число основных, W_М – число местных подвижностей.

Местные подвижности часто предусматривают в механизмах с целью обеспечения более благоприятного распределения нагрузки на звенья и равномерного изнашивания контактирующих поверхностей. При необходимости, местные подвижности можно устранить, повысив класс соответствующих кинематических пар.

Контрольные вопросы

1. Перечислите наиболее часто используемые плоские четырехзвенные рычажные механизмы. Приведите примеры машин или приборов, в которых есть такие механизмы.

2. Чем отличается кривошип от коромысла? Коромысло от кулисы?

3. Что называют степенью свободы механизма?

4. Чем отличается механизм от конструкции?

5. Что означает множитель «6» в структурной формуле Сомова - Малышева?

6. Для каких механизмов используется структурная формула Чебышева?

7. Какие механизмы называют клиновыми? Какую структурную формулу следует использовать для расчета степеней свободы клинового механизма?

8. Что называют местной подвижностью?

9. С какой целью местные подвижности предусматривают в механизмах?

10. Как можно устранить местную подвижность?