Принцип строения рычажных механизмов

Принцип строения рычажных механизмов, сформулированный русским ученым Л.В. Ассуром в 1910 г., состоит в следующем.

· Механизм может быть условно разделен на две основные части: начальный механизм, обладающий подвижностью механизма в целом, и ведомую цепь, подвижность которой относительно звеньев начального механизма равна нулю.

· Ведомая цепь, в свою очередь, может быть разделена на структурные группы звеньев (группы Ассура), каждая из которых обладает нулевой подвижностью.

Принцип Ассура широко применяется в решении задач структурного синтеза, а также в задачах кинематики и динамики механизмов. Структурным группам присваивается класс и порядок. Каждая структурная группа, согласно ее основному свойству, удовлетворяет равенству:

,

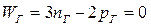где W_Г – число степеней свободы группы, n_Г – число звеньев, p_Г – число кинематических пар группы. Ясно, что данное равенство удовлетворяется при следующих значениях: , , .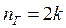

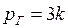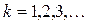По предложению профессора Баранова, число k называется классом структурной группы. Таким образом, двухзвенные группы имеют первый класс, четырехзвенные – второй и т.д. Порядок группы (по Ассуру – Артоболевскому) определяется числом внешних кинематических пар, условно отнесенных к группе, которыми данная группа присоединяется к сопряженным с ней звеньям механизма. Такие кинематические пары принято называть поводками.

Структурных групп первого класса второго порядка существует пять (Рис. 14).

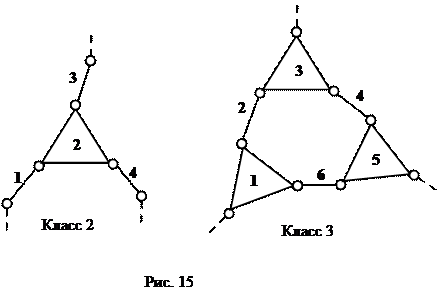
Двухзвенные структурные группы наиболее часто встречаются в используемых на практике рычажных механизмах. Также известны четырех- и шестизвенные структурные группы, которые встречаются в механизмах достаточно редко. Примеры таких групп даны на рис. 15.

Класс механизма определяется наивысшим классом входящих в его состав структурных групп.

Пример

Разделить на структурные группы механизм стана холодной калибровки труб (рис. 16). Данный механизм состоит из шести звеньев (0 – стойка, 1 – кривошип, 2 – шатун, 3 – кулиса, 4 – кулисный камень, 5 – ползун), имеет пять вращательных (0-1, 1-2, 2-3, 3-0, 4-5), одну поступательную (3-4) и одну цилиндрическую (5-0) кинематические пары. Все кинематические пары низшие, механизм – рычажный. Механизм также является плоским, содержит два замкнутых кинематических контура (0-1-2-3-0, 0-3-4-5-0). Число степеней свободы механизма найдем по формуле Чебышева:

.

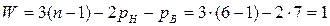Начальный механизм: стойка 0 – кривошип 1 (Рис. 17,а), 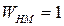; ведомую цепь составляют звенья: 2, 3, 4, 5 (Рис. 17,б).

Ведомая цепь состоит из двух структурных групп первого класса второго порядка: ВВВ (Рис. 17,в) и ПВП (Рис. 17,г).

Контрольные вопросы

1. Какие связи в механизме называют избыточными?

2. Какие избыточные связи могут быть выявлены на уровне кинематической пары?

3. Как определить число контурных избыточных связей?

4. Какими преимуществами и недостатками обладают механизмы с избыточными связями?

5. Сформулируйте принцип строения рычажных механизмов.

6. Перечислите двухзвенные структурные группы. Почему структура ППП не является группой Ассура?

7. Как определяется класс и порядок группы Ассура?