ИСТОЧНИКИ ТОКА 3 страница
Если далее изменять напряженность поля Е, то поляризация Р изменяется по кривой 3 петли гистерезиса (см.рис.4.4).
Сегнетоэлектрические свойства сильно зависят от температуры. Существует определенная для каждого сегнетоэлектрика температура, называемая точкой Кюри, при которой вещество теряет свои особые электрические свойства и кристалл становится обычным полярным диэлектриком.
4.2. Описание установки и метод измерения
Для наблюдения петли гистерезиса сегнетоэлектрика собирают электрическую цепь по схеме, указанной на рис.4.5.
|
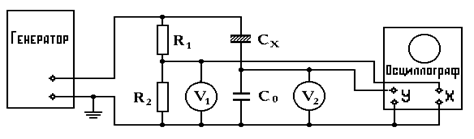
Рис.4.5
Сх -конденсатор с сегнетоэлектрическим диэлектриком (вариконд);
Со -эталонный конденсатор; R1 и R2 -омический делитель напряжения.
Напряжение от звукового генератора (ЗГ) подводится к сегнетоэлектрику через последовательно соединенный с ним конденсатор Со большой емкости. (Со»Сх) Вследствие малого сопротивления перемен- ному току конденсатора Со большая часть напряжения от ЗГ приложена к Сх. Заряды на последовательно соединенных конденсаторах равны, т.е. UоСо = UхСх,
откуда 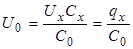 , (4.8)
, (4.8)
которое подается на вертикальный вход осциллографа.
Заряд qх пропорционален вектору электрической индукции в образце:
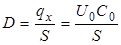 , (4.9)
, (4.9)
где S - площадь пластин конденсатора Сх.
На вертикально отклоняющихся пластинках осциллографа возникает напряжение, пропорциональное электрической индукции D. Так как Сх«С0, то к Сх приложено почти все переменное напряжение, подведенное к схеме. Это напряжение связано с напряженностью электрического поля соотношением
Е = Uх/h, (4.10)
где h - толщина сегнетоэлектрика. Напряжение Uх подается на горизонтально отклоняющие пластины осциллографа с омического делителя R1, R2.
На экране осциллографа возникает картина, изображающая электрические характеристики сегнетоэлектрика в координатах, пропорциональных Е и P (см. формулы (4.4), (4.3), и так как для нашего образца æ » 1, то ε0E « P ≈ D ).
4.3. Порядок выполнения работы
4.3.1. Наблюдение нелинейной поляризации сегнетоэлектрика
на экране осциллографа
1) Подготовить звуковой генератор:
- вывести на минимум (крайнее левое положение)"Регул. выхода";
- установить частоту f = 2кГц;
- соединить выход задающего генератора со стендом.
2) Подготовить осциллограф:
- включить осциллограф тумблером "Сеть";
- перевести ручки "Усиление" координаты Х и "Усиление" координаты У в крайнее левое положение;
- после 5-минутного прогрева осциллографа с помощью ручек "Ось Х" и "Ось У" установить светящееся пятно в центре экрана;
- регуляторами "Яркость" и "Фокус" установить на экране четкое изображение пятна;
- постепенно увеличивая напряжение на выходе генераторе, получить на экране осциллографа петлю гистерезиса с характерным изгибом.
4.3.2. Снятие кривой зависимости вектора поляризации
от напряженности внешнего поля Р = f(Е)
1) Собрать цепь по схеме (см.рис.4.5).
2) Изменяя напряжение Ихэф через 0,2 В, которое подается на горизонтальную ось осциллографа и пропорционально напряженности внешнего поля, поворотом ручки "Рег. выхода" генератора, измерять напряжение Иуэф на конденсаторе Со универсальным вольтметром В7-16.
3) Результаты измерений Ихэф и Иуэф записать в таблицу.
4) Для каждого значения Ихэф определить напряженность Е по формуле (4.10), для каждого значения Иуэф определить значение вектора поляризации Р по формуле (4.9). Для сегнетоэлектриков ε » 1 (а для нашего образца ε ~ 104), электрическая индукция D приблизительно равна Р.
5) Построить график зависимости максимальной поляризации Рмах от величины максимальной напряженности электрического поля Рмах= f(Емах).
6) Для каждого значения Е определить диэлектрическую проницаемость по формуле ε = Р / ( εоЕ) и построить график зависимости ε = f(Е). Значения S и h указаны на передней панели прибора.
4.3.3. Дополнительное задание
1) Найти коэрцитивную силу Еc и остаточную поляризацию Рr, установив для этого максимальную величину напряжения Uх. Определить по осциллографу число делений, соответствующее коэрцитивной силе Еc (отрезок ОЕс на рис.4.4) и умножить ее на цену деления СЕ= 0.6 В/дел. (или указана на передней панели прибора). Найти Uc, коэрцитивную силу рассчитать по формуле Еc = Uc/h.
2) Определить по осциллографу число делений, соответствующее остаточной поляризации Рr (отрезок ОРr на рис.4.4), умножить его на цену деления Сr (значение Сr определяется по положению большой ручки переключателя "Вольт/дел.". Найти Ur. Остаточную поляризацию вычислить по формуле:
Рr= UrСо/S.
4.6. Контрольные вопросы
1. Что называется электрическим диполем, плечом диполя, дипольным моментом?
2. Дайте характеристику диэлектриков с полярными и неполярными молекулами.
3. В чем заключается явление поляризации диэлектрика?
4. Что называется вектором поляризации Р и вектором электрического смещения.
5. Поясните физический смысл диэлектрической проницаемости диэлектрика.
6. Что такое свободные и связанные заряды?
7. Объясните, как происходит поляризация диэлектриков.
8. Чему равен модуль вектора электрического смещения?
9. Что такое сегнетоэлектрики?
10. Дайте понятие доменов и доменной структуры сегнетоэлектриков.
11. В чем заключается явление гистерезиса для сегнетоэлектриков?
12. Что такое коэрцитивная сила и остаточная поляризация? Как они определяются в работе?
13. Как зависят сегнетоэлектрические свойства от температуры?
14. Объясните работу схемы установки.
Литература. [5, §§ 15.1 - 15.5; 6, §§ 80, 87 - 90]
5. ИЗУЧЕНИЕ ЗАВИСИМОСТИ СОПРОТИВЛЕНИЯ МЕТАЛЛОВ
ОТ ТЕМПЕРАТУРЫ С ПОМОЩЬЮ МОСТА УИТСТОНА
Цель работы: экспериментальное исследование зависимости сопротивления медного проводника от температуры и определение температурного коэффициента сопротивления меди.
Приборы и принадлежности: мостик Уитстона, стакан с водой, термометр, электроплитка, металлическая проволока.
5.1. Теоретические сведения
Высокая проводимость металлов обусловлена свободными электронами, несвязанными с отдельными атомами. Известно, что атомы металлов, участвуя в химических реакциях, легко теряют один-два электрона. С изолированными атомами они еще связаны, но когда много одинаковых атомов упаковано в кристалл, эти электроны становятся "собственностью" всей решетки. Сама решетка состоит из положительных ионов, выстроенных правильными жесткими рядами (расстояние между центрами атомов ~ 10-10м). Внутри этой решетки хаотически странствуют "электроны проводимости". В электрическом поле Е они начинают двигаться упорядочено - возникает электрический ток.
То, что за проводимость металлов "отвечают" электроны, впервые доказано экспериментально в 1916 году американским физиком Р.Толменом и шотландским физиком Б.Стюартом. Пусть n - концентрация заряженных частиц (число частиц в 1 м3), e - заряд одной частицы, U - средняя скорость упорядоченного движения частиц. Векторную величину
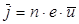
называют плотностью тока. Таким образом, плотность тока численно равна заряду, проходящему за 1 с через поперечное сечение проводника в расчете на 1м2 этого сечения. Сила тока в проводнике
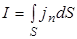 , (5.1)
, (5.1)
где jn = jcosφ - проекция 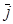 на нормаль n к площадке S (рис.5.1).
на нормаль n к площадке S (рис.5.1).
Одно из самых важных экспериментальных открытий в области электрического тока в веществе выражается законом Ома. Сила тока I, текущего по однородному проводнику, в котором не действуют сторонние силы, пропорциональна разности потенциалов ("напряжению" U) на его концах и обратно пропорциональна сопротивлению проводника R:
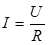 , (5.2)
, (5.2)
При постоянной температуре сопротивление R не зависит от I. Оно зависит от материала, из которого сделан проводник, и очевидным образом связано с длиной проводника L и площадью его поперечного сечения S:
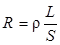 , (5.3)
, (5.3)
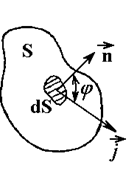 Рис.5.1
Рис.5.1
| Коэффициент ρ - называется удельным сопротивлением и измеряется в Ом∙м (Ом-метр).
Величину σ = 1/ρ называют удельной проводи-мостью. Ее единица - См/м (Сименс на метр).
В твердом изотропном проводнике
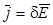 , (5.4)
Выражение (5.4) - закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряжен- , (5.4)
Выражение (5.4) - закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряжен-
|
ностью электрического поля в этой же точке.
Экспериментально установлено, что для металлов зависимость R(t) в области комнатных температур близка к линейной и приближенно может быть представлена в виде
R = Rо(1 + α∆T) = Rо(1 + α∆t) = Rо(1 + αt), (5.5)
где Rо - сопротивление при T = Tо= 273,15 К (температура тающего льда to=0oC); R - сопротивление при температуре t;
∆T = T - Tо = ∆t = t - to = t .
Величину 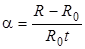 называют температурным коэффициентом сопротивления.
называют температурным коэффициентом сопротивления.
В классической электронной теории металлов предполагалось, что движение электронов подчиняется законам механики Ньютона. Взаимодействие электронов между собой не учитывалось, а взаимодействие электронов с ионами сводилось только к соударению. Иными словами, электроны проводимости рассматривались как электронный газ, подобный идеальному одноатомному газу, для которого справедливо распределение (электронов по скоростям) Максвелла. Средняя кинетическая энергия электронов считается равной энергии атомов, то есть (3/2)∙kТ, где k - постоянная Больцмана, Т - абсолютная температура. Концентрация свободных электронов n по порядку величины сравнима с числом атомов 1 м3. При включении электрического поля Е электроны движутся с одинаковым ускорением 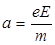 . За время движения электрона между двумя последовательными столкновениями с ионами τ, его скорость изменяется на а∙τ. Предполагается, что при столкновениях с ионами электроны отдают всю энергию, полученную от электрического поля. Для средней скорости упорядоченного движения электронов получаем:
. За время движения электрона между двумя последовательными столкновениями с ионами τ, его скорость изменяется на а∙τ. Предполагается, что при столкновениях с ионами электроны отдают всю энергию, полученную от электрического поля. Для средней скорости упорядоченного движения электронов получаем:
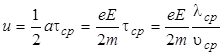 , (5.6)
, (5.6)
где τср и λср - среднее время и средняя длина свободного пробега электронов соответственно, а υср - средняя скорость теплового движения электронов ( 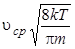 ; при Т = 300 К, υср ≈ 105 м/с).
; при Т = 300 К, υср ≈ 105 м/с).
Подставляя среднюю скорость (5.6) в формулу j = neu, получаем 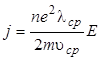 , откуда с учетом формулы (5.4)
, откуда с учетом формулы (5.4) 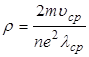
В последнем выражении для ρ средняя скорость υср ~ √Т. Остальные величины от Т не зависят. Таким образом, согласно классической электронной теории ρ ~ √Т, тогда как в эксперименте ρ ~ Т. На пути развития электронной теории металлов встретились и другие трудности, преодолеть которые удалось лишь с помощью квантовой механики.
Квантовая теория дает правильную зависимость R(Т) ~ Т металлов. Она объясняет и такое универсальное явление, как сверхпроводимость некоторых металлов и сплавов при низких температурах.
5.2. Описание установки
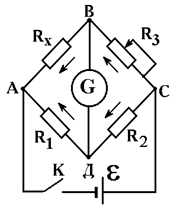 Рис.5.2
Рис.5.2
| Принципиальная схема мостика Уитстона - прибора для измерения сопротивления - приведена на рис.5.2. Сопротивления R1, R2, R3 и Rх образуют замкнутый четырехугольник ABCD. В диагональ AC включен источник постоянного тока ε, в другую диагональ - чувствительный гальванометр G. Если ток через гальванометр равен нулю, то говорят о равновесии моста. При этом φв= φд, I1 = I2, Iх = I3, I1R1 = IхRх, I2R2 = I3R3. |
Откуда 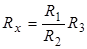 . (5.7)
. (5.7)
В данной установке в качестве R3 используется магазин сопротивлений и его можно изменять через 0,1 Ом. Сопротивления R1 и R2 постоянны и расположены внутри корпуса сопротивлений R3. Гальвано- метр, имеющий нуль посредине шкалы, и кнопка К также смонтированы на корпусе R3. В данной установке R1 =R2 и условие равновесия моста принимает вид:
Rх = R3 . (5.8)
Таким образом, если Rх - неизвестное сопротивление, то его можно определить согласно формуле (5.8), подобрав R3 так, чтобы IG= 0.
Для этого устанавливают R3 примерно равным Rх при комнатной температуре (с целью избежания большого IG, что может привести к выходу гальванометра из строя). Начальное значение R3 указано на установке. Нажимая кнопку К (вначале кратковременно), проверяют положение стрелки гальванометра и, изменяя R3, ставят ее на нуль. При этом Rх= R3.
В данной работе Rх - сопротивление медной проволоки, которая намотана на диэлектрический стержень и помещена в пробирку. Клеммы для подключения концов Rх находятся на корпусе R3.
5.3. Порядок выполнения работы
1) Опустить пробирку с Rх и термометр в стакан с холодной во- дой, через 3...5 минут произвести первое измерение Rх.
2) Стакан с водой поставить на электроплитку, включенную в сеть ~ 220В.
3) По мере нагревания воды производить измерения Rх примерно через каждые 10 К. При этом стакан вместе с сопротивлением и термометром сначала снимается с электроплитки, и лишь спустя 2...3 минуты производится измерение. Пауза делается для того, чтобы избежать "отставания" температуры проволоки от температуры воды. Пауза не делается в том случае, если медная проволока помещена в пробирку с трансформаторным маслом.
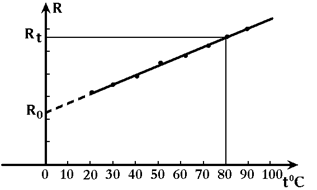 Рис.5.3 Рис.5.3
| 4) Построить график R = R(t), изображенный на рис.5.3, отклады-вая по горизонтальной оси t от 0oC до 100oC с масштабом 1oC в 1 мм, а по вертикальной оси R так, чтобы все измерения ∆R от начальной температуры до t = 100oC также пришлись примерно на 100мм. 5) Экстраполируя график R(t) до пересечения с осью R (см.рис.5.3), |
определить Rо при 0оС и Rt при температуре t. По формуле α = (Rt- Ro)/(Rot) рассчитать температурный коэффициент сопротивления меди.
6) Найти основные источники погрешности при определении α и оценить точность, с которой получена его величина.
5.4. Контрольные вопросы
1. Какие частицы являются носителями тока в металле?
2. Что такое сопротивление? Какова единица измерения сопротивления?
3. Как сопротивление металлов зависит от температуры? Дайте качественное объяснение.
4. Как в данной работе определяется Rо?
5. Что такое температурный коэффициент сопротивления?
6. Выведите условия равновесия моста.
7. Почему в данной работе используется гальванометр с двухсторонней шкалой?
8. Что такое плотность тока?
9. Сформулируйте закон Ома в дифференциальной форме.
Литература. [1, §§ 69,70; 2, §§ 34,78; 4, §§ 15,19-21].
6. ИЗМЕРЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ
Цель работы: экспериментальное измерение скорости звука в воздухе при комнатной температуре с помощью электронного осциллографа и проверка формулы для скорости звука в газах.
Приборы и принадлежности: электронный осциллограф, звуковой генератор, телефон, микрофон, соединительные провода.
6.1 Теоретические сведения
Если в каком-либо месте упругой среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами эти колебания будут распространяться от частицы к частице с некоторой скоростью υ Процесс распространения колебаний в пространстве называют волной.
Упругие волны, имеющие частоту в пределах от 16 до 20000 Гц, - это звуковые волны или просто звук. Упругая волна называется продольной, если смещение частиц происходит из положения равновесия в направлении распространения волны. Если же частицы колеблются в плоскостях, перпендикулярных направлению распространения волны, то волну именуют поперечной. Упругие поперечные волны возникают лишь в среде, способной сопротивляться сдвигу. Таким свойством обладают только твердые тела. Продольные волны могут распространяться в любой упругой среде - твердой, жидкой и газообразной.
Время Т одного полного колебания называют периодом. Расстояние λ, на которое распространяется волна за один период - это длина волны. Если υ - скорость волны, то очевидно
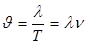 , (6.1)
, (6.1)
где ν - частота колебаний.
Уравнение бегущей волны - это зависимость смещения ξ колеблющейся частицы от координат x,y,z ее равновесного положения и времени t: ξ = ξ(x,y,z,t). Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны. В простейшем случае фронт волны представляет собой плоскость, соответственно волна в этом случае называется плоской.
Рассмотрим плоскую гармоническую волну, распространяющуюся в направлении X. Пусть в точке х=0 функция ζ имеет вид
ζ(0,t) = Aоcosωt ,
где ω = 2π∕T - циклическая (или круговая) частота;
Ао - амплитуда смещения частиц при х = 0.
Расстояние от точки х = 0 до точки х волна пройдет за время τ = х/υ. Следовательно, колебания частиц, лежащих в плоскости x, будут отставать по времени на τ от колебаний частиц в плоскости х = 0. Таким образом, уравнение плоской гармонической волны, распространяющейся в направлении X, имеет вид:
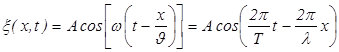 , (6.2)
, (6.2)
где А - амплитуда колебаний частиц в плоскости х.
Аргумент 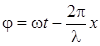 называют в данном случае фазой волны.
называют в данном случае фазой волны.
В соответствии с уравнением (6.2) длину волны λ можно определить еще как расстояние между ближайшими точками, в которых колебания отличаются по фазе на 2π.
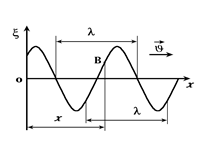 Рис.6.1 Рис.6.1
| На рис.6.1 показано смещение частиц среды ξ в зависимости от их равновесного положения х в фиксированный момент времени t (в газе частицы колеблются только вдоль х!). Отметить, что смещение частиц из положения равновесия в звуковой волне весьма незначительно. Так, например, при болезненно громком звуке на частоте 440 Гц А ≈ 0,25 мм, а на пороге слышимости А ≈ 10-7мм. Таким образом, человеческое ухо |
настолько чувствительно, что может воспринимать смещения барабанной перепонки, равные диаметру атома.
Очень большие значения могут достигать ускорения частиц в звуковой волне. Амплитуде смещения А = 0,25 мм при частоте 440 Гц со- ответствует амплитуда ускорения В = ω2А = (2π)2∙ 4402∙10-3/4 = 1,91∙104(м/с2) ≈ 2000g (g - ускорение свободного падения). Звуковое давление (превышение давления над равновесным значением) в этом случае будет равно: Рзв ≈ 65 Н/м2.
Величина скорости звуковых волн зависит от упругих свойств среды. В газах скорость звука близка к средней скорости молекул и составляет при нормальных условиях несколько сотен метров в секунду (наибольшая скорость у водорода ~ 1200 м/с). Скорость звука в жидкостях колеблется от 1 до 2 км/с. Скорость упругих волн в твердых телах доходит до 5...6 км/с, а в алмазе имеет рекордное значение 18 км/с, превосходя третью космическую скорость.
Скорость звука в газах определяется формулой
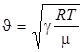 , (6.3)
, (6.3)
где R - универсальная газовая постоянная;
T - абсолютная температура;
μ - молекулярная масса;
γ= Сp/Сv - коэффициент Пуассона.
Основным элементом электронного осциллографа является электронно-лучевая трубка, схематически показанная на рис.6.2.
Подогреваемый катод К является источником электронов, которые ускоряются электрическим полем в промежутке между катодом К и анодом А. Узкий пучок быстрых электронов падает затем на экран Э трубки, покрытый флуоресцирующим составом. В месте падения возникает яркое пятно (точка).
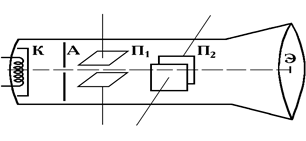 Рис.6.2.
Рис.6.2.
|
На пути электронного луча помещают две пары взаимно перпендикулярных пластин П1 и П2. Если на горизонтальные пластины П1 подать переменное напряжение, то электронный луч будет отклоняться вверх-вниз. И соответственно точка на экране будет перемещаться по вертикальной линии (при частоте более 10 Гц на экране будет видна вертикальная светящаяся черта). Аналогично при подаче переменного напряжения на вертикальные пластины П2 светлая точка на экране будет двигаться по горизонтальной линии. При одновременной подаче переменных напряжений на пластины П1 и П2 точка на экране будет двигаться в двух взаимно перпендикулярных направлениях, "рисуя" на экране ту или иную линию.
6.2. Метод измерения
В данной работе непосредственно измеряется длина звуковой волны λ при заданной частоте ν. Затем по формуле (6.1) определяется скорость звука. В основе метода измерений λ лежит теория сложения двух взаимно перпендикулярных колебаний одинаковой частоты.
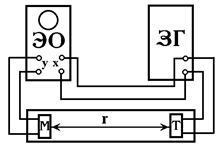 Рис.6.3
Рис.6.3
| Электрические колебания частоты ν от звукового генератора ЗГ (рис.6.3) подаются на телефон Т, возбуждая механические колебания мембраны телефона с той же частотой. Эти колебания распространяются по воздуху в виде звуковой волны. Одновременно электрическое напряжение частоты ν от ЗГ подается на горизонтальные пластины ЭО. Звуковые волны, попадая на |
микрофон М, возбуждают механические колебания его мембраны, которые преобразуются в электрические колебания той же частоты ν и подаются на вертикальные пластины ЭО.
На экране ЭО светящаяся точка участвует в двух взаимно перпендикулярных колебаниях одинаковой частоты ν (или ω). Уравнения этих колебаний имеют вид
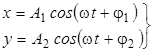 (6.4)
(6.4)
где φ1 и φ2 - начальные фазы колебаний.
Чтобы получить траекторию светящейся точки (т.е. связь между x и y) на экране осциллографа, исключим из выражения (6.4) время. Обозначим ωt+φ1=α, φ2-φ1=β. Тогда 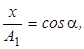
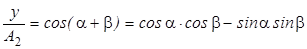 или
или
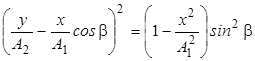
После возведения в квадрат левой части и приведения подобных членов получим:
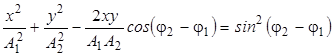 (6.5)
(6.5)
В общем случае выражение (6.5) - уравнение эллипса. Если φ2-φ1= (2n+1)∙π/2, где n = 0,1,2,..., точка на экране будет двигаться по эллипсу, симметрично относительно координатных осей (рис.6.4). При А1= A2 эллипс вырождается в окружность. При φ2-φ1= 2πn, где n = 0,1,2,...,
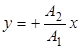 (6.6)
(6.6)
и на экране будет прямая, лежащая в 1-м и 3-м квадрантах (рис.6.5).
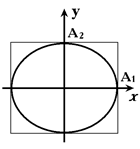 Рис.6.4
Рис.6.4
| 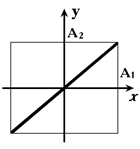 Рис.6.5
Рис.6.5
| 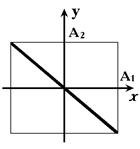 Рис.6.6
Рис.6.6
|
При φ2- φ1= (2n+1)π, где n =0,1,2,...,
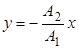 (6.7)
(6.7)
и прямая на экране осциллографа находится во 2-м и 4-м квадрантах (рис.6.6).
Изменению расстояния между телефоном и микрофоном на ∆r соответствует изменение разности фаз напряжений на пластинах П1 и П2 (см.рис.6.2).
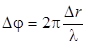 (6.8)
(6.8)
В частности, при ∆r =λ и ∆φ = 2π картина на экране ЭО повторяется. Наиболее точные измерения получаются, когда при начальном и конечном положении микрофона на экране наблюдаются прямые линии. Тогда скорость звука определяется по формуле.
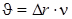 (6.9)
(6.9)
6.3. Порядок выполнения работы
1) Собрать установку, блок-схема которой представлена на рис.6.3.
2) Включить в сеть звуковой генератор и осциллограф. На лимбе звукового генератора выставить рабочую частоту. Подать напряжение на телефон. Ручками "усиление" на панели осциллографа добиться, чтобы амплитуды складываемых колебаний были примерно одинаковыми.
3) Перемещая микрофон вдоль скамьи, добиться получения на экране осциллографа изображения прямой линии (рис.6.5 или 6.6), занести его в тетрадь и отметить положение микрофона r1. Затем переместить микрофон в положение r2 на кратчайшем расстоянии от r1, при котором на экране возникает та же картина. В этом случае изменение разности фаз равно 2π и ∆r = r2- r1 = λ. Повторить опыт при трех различных r1.
Дата добавления: 2015-03-03; просмотров: 766;
