ИСТОЧНИКИ ТОКА 1 страница
Составители: Л.А.Григорьев, Т.И.Краева, В.П.Медведчиков,
Н.Г.Грунина, А.С.Шилова, Е.Ф.Козяев
УДК 531 / 076.5 / : 378
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ: Методические указания к выполнению лабораторных работ для студентов всех специальностей / Сост. Л.А.Григорьев, Т.И.Краева, В.П.Медведчиков и др.; Под ред. Л.А.Григорьева. - Йошкар-Ола: МарГТУ, 2001. - 52 с.
Приведены лабораторные работы по разделу "Электричество" курса
общей физики. Каждая работа содержит краткое теоретическое описание изучаемого явления, описание установки, порядок выполнения работы, обработки результатов измерений и вопросы самопроверки.
Рис.32. Библиогр. 7 назв.
Печатается по решению редакционно-издательского совета МарГТУ
Рецензент - А.С.Масленников, канд.физ.-мат.наук, доцент МарГТУ
© Марийский государственный
технический университет, 2001
ВВЕДЕНИЕ
Методические указания включают в себя шесть работ из лабораторного практикума по разделу "Электричество" и соответствуют учебному плану.
Цель практикума заключается в том, чтобы позволить студенту самому воспроизвести основные физические явления, научить его обращаться с основными электроизмерительными приборами, познакомить с важнейшими методами измерений.
При выполнении работ студенты знакомятся с принципами работы электроизмерительных приборов, электрическими полями различной конфигурации, действием электрического поля на пучок электронов в электронно-лучевой трубке осциллографа; изучают свойства системы двух проводников накапливать заряды, свойства диэлектрика влиять на электростатическое поле; исследуют зависимость сопротивления проводника от температуры, зависимость диэлектрической проницаемости сегнетоэлектриков от величины напряженности внешнего электрического поля; овладевают методами расчета погрешности электрических величин, моделирования при изучении электростатического поля, измерения емкости с помощью баллистического гальванометра, сложения двух взаимно перпендикулярных колебания для измерения скорости звука.
Не менее существенно закрепить навыки ведения лабораторной тетради, построения графиков и оценки полученных результатов.
Описания к работам начинаются с теоретических введений. Они составлены так, чтобы ясное представление об изучаемых явлениях могли себе составить как студенты, которые уже прослушали этот материал на лекциях, так и те, кто только приступает к изучению соответствующего раздела физики.
После теоретических введений приводятся описания измерительной аппаратуры и применяемого метода измерений. Затем следуют задания, регламентирующие последовательность работы студентов при проведении измерений и обработки полученных результатов. Задания определяют только тот необходимый минимум, без выполнения которого работа не может считаться выполненной.
Методические указания предназначены для студентов 1 - 2 курсов всех специальностей.
1. ЗНАКОМСТВО С ЭЛЕКТРОИЗМЕРИТЕЛЬНЫМИ ПРИБОРАМИ
Цель работы: знакомство с принципом работы электроизмерительных приборов и их условными обозначениями. Определение погрешности электрических измерений.
Принадлежности: набор электроизмерительных приборов разных систем, таблицы принятых обозначений.
1.1. Теоретические сведения
В соответствии с ГОСТ 232117-78 для электроизмерительных приборов с непосредственным отсчетом установлены следующие условные обозначения, наносимые на них:
А. Основные единицы измерения (по роду измеряемой величины), либо их кратные или дольные значения:
| A | - Ампер | mA | - миллиампер | μA | - микроампер |
| V | - Вольт | kV | - киловольт | mV | - милливольт |
| W | - Ватт | kW | - киловатт | MW | - мегаватт |
| Ω | - Ом | kΩ | - килоом | MΩ | - мегаом |
| Hz | - Герц | kHz | - килогерц | MHz | - мегагерц |
Б. Род тока: постоянный, обозначается знаком —, переменный ~, постоянный и переменный 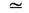 , трехфазный
, трехфазный 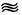 .
.
В. Безопасность: внутри пятиконечной звездочки указываетсянапряжение в киловольтах, при котором проверена изоляция прибора.
Например:

| - испытательное напряжение 2 кВ; - испытание изоляции не предусмотрено; - испытательное напряжение 500 В. |
Г. Используемое положение:
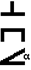
| - вертикальное положение шкалы; - горизонтальное положение шкалы; - прибор применять при наклонном (под углом a к горизонту) положении. |
Д. Класс точности: указывается на приборе соответствующей цифрой, например, 0.5; 1.0; 1.5; и т.д. или  ,
,  .
.
Е. Общие условные обозначения принципа действия электроизмери-тельных приборов:

| - прибор магнитоэлектрической системы с подвижной рамкой; - прибор электромагнитный; |

| - прибор электродинамический; - прибор электростатический |
З. Обозначения зажимов:
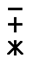
| - отрицательный зажим; - положительный зажим; - общий зажим (для многопредельных приборов переменного тока и комбинированных приборов); |
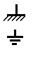
| - зажим, соединенный с корпусом; - зажим для заземления |
При необходимости значение того или иного символа следует уточнить в справочнике или таблице, которая имеется в лаборатории.
Все внешние части средств измерений, находящиеся под напряжением, превышающим 32 В по отношению к корпусу, должны быть защищены от случайных прикосновений к ним, т.е. иметь защитные кожухи, утопленные гнезда, клеммы с изоляционными головками и т.д.
Средства измерений с питанием от сети должны иметь сетевую индикацию включения сетевого выключателя. В цепи питания прибора должен быть плавкий предохранитель с указанием силы тока.
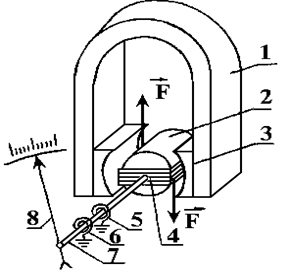 Рис.1.1
Рис.1.1
| Принцип действия приборов магнитоэлектрической системы основан на взаимодействии подвижной катушки с током с полем постоянного магнита. На рис.1.1 схематически показано устройство такого прибора. В нем магнитное поле создается постоянным магнитом 1 подковообразной формы. Полюсные наконечники 3 обращены друг к другу вогнутыми цилиндрическими поверхно-стями одинаковых радиусов. Между полюсами укреплен железный цилиндр2 меньшего радиуса. В зазоре, где магнит-ное поле радиально, плотность магнитного потока равномерная, а магнитная индукция |
постоянная, расположена легкая рамка 4, состоящая из нескольких витков ровода, концы которого присоединены к спиральным пружинам 5 и 6. Через эти пружины в рамку подается измеряемый ток. При прохождении тока через рамку на нее действует вращательный момент, рамка поворачивается вокруг оси 7, пружины 5 и 6 закручиваются, и создается противодействующий момент. При равновесии моментов рамка устанавливается неподвижно, а соединенная с рамкой стрелка 8 указывает угол поворота. Значение этого угла пропорционально силе измеряемого тока, поэтому шкала прибора равномерная.
По указанному принципу изготовляется большинство лабораторных и технических приборов постоянного тока. Их можно использовать, например, в качестве амперметров, включая параллельно рамке шунт, или в качестве вольтметров, включая последовательно с рамкой большое добавочное сопротивление.
Принцип действия приборов электромагнитной системы основан на взаимодействии ферромагнитного сердечника с магнитным полем катушки с током. Амперметр такой системы схематически показан на рис.1.2, где К - катушка, по которой течет измеряемый ток; a - железный стержень, подвешен-ный на пружине П. Катушка с током I создает неоднородное магнитное поле с индукцией В, при этом на стержень a действует сила F ~ М(¶В/¶z), где М – намагниченность стержня, z - ось катушки и стержня. Эта сила втягивает
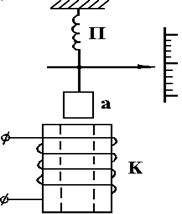 Рис.1.2
Рис.1.2
| стержень в катушку и уравновешивается силой упругости пружины П. Со стержнем связана стрелка. Каждому значению силы тока I соответствует определенное положение стрелки прибора. Между F и J нет линейной зависимости, поэтому шкала прибора оказывается неравно-мерной. Приборы электромагнитной системы просты, недороги, они могут использоваться как в цепях постоянного тока, так и в цепях переменного тока промышленной частоты. Однако точность их невысока. |
В приборах электродинамической системы используется взаимодействие двух катушек с токами. Одна из них неподвижна. Магнитное поле B1, создаваемое этой катушкой, пропорционально силе тока I1. Вторая, подвижная катушка, состоит из большого числа витков тонкой проволоки. На оси этой катушки закреплены стрелка прибора и легкие спиральные пружины, противодействующие повороту катушки.
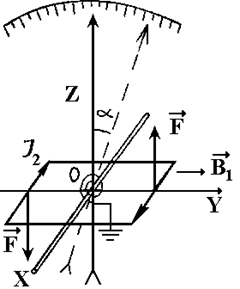 Рис.1.3
Рис.1.3
| На рис.1.3 показана схема, поясняющая принцип работы электродинамического прибора. Подвижная катушка изображена в виде рамки с током I2. Плоскости витков неподвижной катушки параллельны пло-скости OXZ (сама неподвижная катушка на рисунке не показана), при этом магнитное поле B1 направлено вдоль оси OY. При прохождении через подвижную катушку из-меряемого тока I2 на последнюю действует момент сил, пропорциональный силе тока I2 и магнитному полю B1. Этот момент уравновешивается моментом сил упругости пружины. Угол поворота стрелки оказывается при этом пропорциональным |
произведению силы тока в катушках: a ~I1×I2.
Электродинамическими приборами можно измерять электрический ток, напряжение и мощность в цепи как постоянного, так и переменного тока.
В настоящее время широкое распространение получили цифровые измерительные приборы (ЦИП), которые автоматически вырабатывают дискретные сигналы измерительной информации и представляют показания в цифровой форме. Среди ЦИП есть приборы, показывающие мгновенное значение измеряемой величины, и приборы, фиксирующие среднее значение величины за определенный промежуток времени ∆t, т.е. интегрирующие.
Пусть x - измеряемая величина (сила тока, напряжение, сопротивление и т.п.). Шкала прибора разбивается на то или иное число делений и служит для отсчета x. Возле делений ставят цифры, которые обозначают либо число делений, либо непосредственно значение x.
Значение xн (номинальное значение x), приводящее к отклонению стрелки на всю шкалу, соответствует пределу измерений. Прибор может иметь либо один, либо несколько пределов измерений (или поддиапазонов).
Чувствительностью прибора называют величину, равную отношению изменения сигнала на выходе измерительного прибора к вызывающему его изменению измеряемой величины:
S = ∆l / ∆x,
где ∆x - изменение измеряемой величины,
∆l - изменение сигнала на выходе.
Порог чувствительности - это изменение измеряемой величины, вызывающее наименьшее перемещение указателя прибора, которое еще можно заметить при нормальном для прибора способе отсчета.
Чувствительность цифрового прибора определяется как значение измеряемой величины, приходящееся на единицу дискретности (на единицу наименьшего разряда поддиапазона).
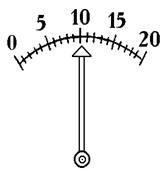 Рис.1.4
Рис.1.4
| Ценой деления называют величину С = xк/n, где n - число делений шкалы. Для отсчета x по шкале надо, очевидно, цену деления умножить на число отсчитанных от начала шкалы делений. Пусть, например, шкала прибора имеет 20 делений (рис.1.4), а предел измерений - 10 В. При отклонении стрелки на 10 делений получим для напряжения: U = (xк/n)10 = (10/20)10 = 5 (В) |
1.2. Оценка погрешностей электрических измерений
Разность между показаниями прибора хп и действительным значением хд называют абсолютной погрешностью измерительного прибора:
∆x = хп- хд.
Таким образом, если хп - показание прибора, то можно лишь утверждать, что
хд = хп ± ∆x.
По значению абсолютной погрешности нельзя судить о точности измерений. Так, например, если ∆x = 1 А при х = 100 А считать высокой точностью, то вряд ли можно считать ее таковой при х = 1 А. Поэтому вводят понятие относительной погрешности δ – отношение абсолютной погрешности к действительному значению измеряемой величины:
δ = ∆x/хд или δ = (∆x/хд)∙100%.
Но данная характеристика непригодна для нормирования погрешности прибора, так как δ = ∞ при х = 0. Для этих целей используют приведенную погрешность:
δпр = ∆x/хк,
где хк - соответствует пределу измерений.
Точность ряда приборов можно сравнивать только по приведенным (нормированным) погрешностям.
На практике вместо истинного значения хд используют хп (показание прибора). Способ определения ∆x должен быть известен заранее. Для этого на каждом приборе указывается класс точности в виде числа, например, 4; 2.5; 1.5; 1.0; 0.5; 0.1 и т.д.
Класс точности прибора показывает, сколько процентов составляет абсолютная ошибка ∆х от предела измерений хк. Таким образом, класс точности равен (∆х/хк)∙100%, откуда легко найти ∆х.
Рассмотрим пример. Пусть предел измерений амперметра - 20 А (Iк= 20 А), на приборе указан класс точности - 1,5. Значит
(∆I/Iк)∙100 = 1,5 и ∆I = 1,5∙20/100 = 0,3 (А)
Таким образом, при любом (!) показании амперметра Iп для действительного значения силы тока имеем:
I = (Iп ± 0,3) А,
Например: если Iп = 3 А, то I = (3 ± 0,3) А;
если Iп = 12 А, то I = (12 ± 0,3) А.
В том случае, когда прибор многопредельный, класс точности, указанный на приборе, относится к каждому пределу. Пусть, например, вольтметр имеет два предела измерения - 1 В и 10 В, а класс точности его - 2,5. Тогда при измерениях на первом пределе ∆U = 0,025 В, а при измерениях на втором пределе ∆U = 0,25 В.
Так как относительная ошибка измерений δ = ∆x/xп, ясно, что при наличии нескольких пределов измерений выбирать надо наименьший, при котором стрелка прибора еще "не зашкаливает".
Если указываемый прибором класс точности обведено кружком, например  , то это означает, что абсолютная погрешность составляет 1.5 % от данного показания прибора, а не от конечного значения шкалы хк.
, то это означает, что абсолютная погрешность составляет 1.5 % от данного показания прибора, а не от конечного значения шкалы хк.
Приборы класса точности до 0,5 включительно применяются для точных измерений и называются прецизионными.
Для цифровых измерительных приборов относительная погрешность δ
определяется по формуле
δ = [c + d(|хк/хп| - 1)],
где с и d - постоянные числа, %;
хк - конечное значение величины в данном поддиапазоне;
хп - показание прибора.
Значения с и d указываются в паспорте прибора для каждого поддиапазона. Так, например, если с = 0.02, d = 0.01, хк= 1.000 В, хп= 0.500 В, то
δ= [0.02 + 0.01(|1.000/0.500| - 1)] = ± 0.03
δ = ± 0.03 %.
1.3. Порядок выполнения работы
1. Дать краткое описание одного стрелочного прибора (многопредельного) в соответствии с обозначениями и символами, указанными на шкале.
2. Определить цену деления и максимальную абсолютную ошибку для каждого предела измерений, привести три примера отсчета измеряемой величины при различных положениях стрелки.
3. Определить относительную ошибку цифрового прибора для одного из поддиапазонов при двух значениях измеряемой величины (по указанным значениям с, d и хк).
1.4. Контрольные вопросы
1. Какие основные условные обозначения применяются для классификации электроизмерительных приборов?
2. Как работает электроизмерительный прибор магнитоэлектрической системы?
3. Каков принцип действия приборов электромагнитной системы?
4. Поясните устройство и принцип действия приборов электродинамической системы.
5. Какие приборы получили в настоящее время широкое распространение?
6. Какую величину называют чувствительностью измерительного прибора?
7. Как определяется ценя деления?
8. Что такое класс точности измерительного прибора?
9. Как на практике рассчитывается абсолютная погрешность измерительного прибора?
10. Как рассчитать относительную погрешность прибора при любом положении стрелки?
Литература. [7 гл.1.2]
2. ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы: экспериментальное исследование электростатического поля методом электростатической ванны и описание его при помощи силовых линий и поверхностей равного потенциала.
Принадлежности: специальная установка, набор сменных электродов
2.1. Теоретические сведения
2.1.1. Закон Кулона. Напряженность электрического поля
Взаимодействие точечных зарядов q1и q2 описывает экспериментальный закон Кулона:
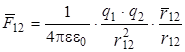 , (2.1)
, (2.1)
где 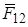 - сила, действующая на q1 со стороны q2;
- сила, действующая на q1 со стороны q2;
r12 - расстояние между зарядами;
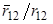 - единичный вектор направленный от q2 к q1;
- единичный вектор направленный от q2 к q1;
eо - диэлектрическая постоянная, определяемая из опыта;
e - диэлектрическая проницаемость среды (для вакуума e=1, для диэлектриков e>1).
Опыт показывает, что при наличии зарядов q1, q2, q3,..., результирующая сила 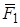 , действующая со стороны поля на заряд q1, равна векторной сумме сил
, действующая со стороны поля на заряд q1, равна векторной сумме сил 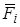 , приложенных к нему со стороны каждого из зарядов qi:
, приложенных к нему со стороны каждого из зарядов qi:
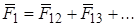 , (2.2)
, (2.2)
где 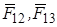 ,... определяются по закону Кулона (2.1).
,... определяются по закону Кулона (2.1).
Напряженность электрического поля в данной точке есть векторная величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:
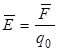 , (2.3)
, (2.3)
где 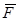 - сила, действующая на пробный заряд qо, помещенный в рассматриваемую точку пространства. В частности, напряженность поля точечного заряда q определяется в соответствии с законом Кулона (2.1) по формуле:
- сила, действующая на пробный заряд qо, помещенный в рассматриваемую точку пространства. В частности, напряженность поля точечного заряда q определяется в соответствии с законом Кулона (2.1) по формуле:
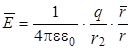 , (2.4)
, (2.4)
где 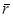 - вектор, проведенный от точечного заряда q в данную точку.
- вектор, проведенный от точечного заряда q в данную точку.
Поле, создаваемое неподвижными относительно выбранной системы отсчета зарядами, называется электростатическим.
Если поле создается точечными зарядами q1, q2,..., то согласно выражению (2.2) имеет место принцип суперпозиции полей:
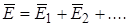 , (2.5)
, (2.5)
где 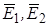 ,... - напряженность полей, создаваемых в данной точке каждым из зарядов q1, q2,... в отдельности, а Е - суммарная напряженность результирующего поля.
,... - напряженность полей, создаваемых в данной точке каждым из зарядов q1, q2,... в отдельности, а Е - суммарная напряженность результирующего поля.
2.1.2. Работа в электростатическом поле. Потенциал
На заряд qо в электростатическом поле Е действует сила F = qоЕ, и, следовательно, при его перемещении совершается работа. Рассмотрим электростатическое поле, создаваемое точечным зарядом q, и найдем работу, совершаемую (силами поля) при перемещении заряда qо из точки 1 в точку 2 (рис.2.1). Для определенности возьмем заряды q и qо одного знака. На элементарном участке пути dl совершается работа
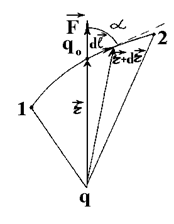 Рис.2.1
Рис.2.1
| 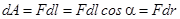 и и 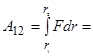
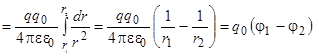 , (2.6)
где потенциал φ в точке электростатического поля определяется точечным зарядом q и расстоянием r от него до точки: , (2.6)
где потенциал φ в точке электростатического поля определяется точечным зарядом q и расстоянием r от него до точки:
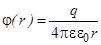 (2.7) (2.7)
|
Таким образом, работа по перемещению заряда qо в поле неподвижного точечного заряда q не зависит от выбора траектории и определяется только его начальным и конечным положением. В частности, работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому контуру L, равна нулю, т.е.
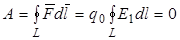
Так как qо ≠ 0, то 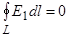 . (2.8)
. (2.8)
Величину 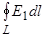 называют циркуляцией вектора Е по замкнутому контуру L . Согласно формуле (2.8) для электростатического (!) поля точечного заряда характерным является то, что в нем циркуляция Е по любому замкнутому контуру равна нулю (электростатическое поле потенциальное, а электростатические силы консервативные).
называют циркуляцией вектора Е по замкнутому контуру L . Согласно формуле (2.8) для электростатического (!) поля точечного заряда характерным является то, что в нем циркуляция Е по любому замкнутому контуру равна нулю (электростатическое поле потенциальное, а электростатические силы консервативные).
Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу А12 можно представить как разность потенциальных энергий, которыми обладает заряд qо в начальной и конечной точках поля заряда q:
А12 = W1 - W2. (2.9)
Принято говорить просто об энергии заряда qо в электростатическом поле. Сравнивая выражения (2.9) и (2.6), получаем
φ(r) = W/qо. (2.10)
В силу принципа суперпозиции формулы (2.8) - (2.10) остаются справедливыми и в случае, когда электростатическое поле создается зарядами q1, q2,... . При этом Е = E1+ E2+ ... и φ =φ1+ φ2+ ... в каждой точке.
Величину φ называют потенциалом поля в данной точке. Согласно выражению (2.10) потенциал в точке электростатического поля равен потенциальной энергии, которую имел бы единичный положительный заряд, помещенный в эту точку . В частности, потенциал поля точечного заряда определяется формулой (2.7). Из выражения (2.10) получаем единицу потенциала : 1В = 1Дж /1Кл. Для разности потенциалов в точках 1 и 2 имеем:
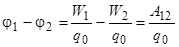 (2.11)
(2.11)
Таким образом, разность потенциалов в двух точках равна работе, совершаемой полем при перемещении единичного положительного заряда из начальной точки в конечную.
Работа сил поля при перемещении заряда qо из точки 1 в точку 2 может быть записана также в виде
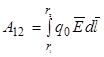 (2.12)
(2.12)
Из формул (2.11) и (2.12) вытекает выражение для разности потенциалов:
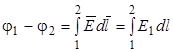 ,(2.13)
,(2.13)
где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки.
2.1.3. Связь между напряженностью Е и потенциалом j
Рассмотрим произвольное направление 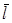 (рис.2.2). Из выражения (2.13)
(рис.2.2). Из выражения (2.13)
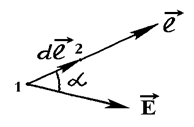
 Рис.2.2 Рис.2.2
| при условии, что точки 1 и 2 рас- j положены бесконечно близко друг к другу, имеем:
j1-j2 = -(j2-j1) = -dj = Еdlcosa = Еldl
или 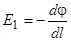 (2.14)
Отсюда часто используемая единица измерения - В/м. (2.14)
Отсюда часто используемая единица измерения - В/м.
|
В частности, 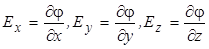
Вектор с проекциями 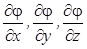 на оси x, y, z соответственно называют градиентом скалярной функции j (x,y,z) и обозначают gradj.
на оси x, y, z соответственно называют градиентом скалярной функции j (x,y,z) и обозначают gradj.
Таким образом, 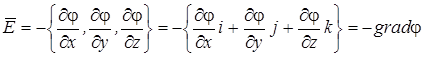 (2.15)
(2.15)
Пусть точка О - любая (фиксированная) точка поля, а М - произвольная точка сферы бесконечно малого радиуса ρ с центром в точке О(рис.2.3). По определению разности потенциалов,
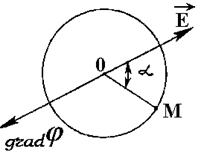 Рис.2.3
Рис.2.3
| φ(O) - φ(M) ≡ Е(O)ρ cosα. (2.16) Эта разность, очевидно, максимальна при α1= 0, то есть при перемещении из точки О вдоль вектора напряженности Е, и мини- Рис.2.3 мальна при α2= π, то есть при перемещении из точки О вдоль вектора -Е = grad φ. Таким образом, gradφ направлен в сторону максимального роста, а вектор напряженности Е |
- в сторону максимального убывания потенциала φ(x,y,z).
Для графического изображения полей пользуются силовыми линиями. Силовая линия проводится так, что касательная к ней в каждой точке совпадает с прямой, вдоль которой направлен вектор напряженности Е в этой точке. Этим линиям приписывают направление, совпадающее с направлением вектора напряженности Е.
Плотность силовых линий, то есть число силовых линий, пронизывающих площадку в 1 м2, расположенную перпендикулярно к ним, выбирают равной величине Е. Таким образом, с помощью силовых линий можно графически изобразить и величину, и направление вектора напряженности Е.
Эквипотенциальной называют поверхность, все точки которой имеют одинаковый потенциал φ(x,y,z) = const. Очевидно, в каждой точке такой поверхности вектор Е перпендикулярен к этой поверхности (рис.2.4), следовательно, силовые линии ортогональны к эквипотенциальным поверхностям.
Эквипотенциальные поверхности обычно строят так, чтобы разности потенциалов между любыми двумя соседними поверхностями были одинаковыми (рис.2.5). Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше.
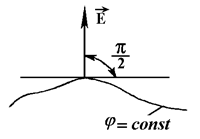 Рис.2.4
Рис.2.4
| 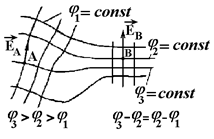 Рис.2.5
Рис.2.5
|
Зная расположение эквипотенциальных поверхностей, можно построить силовые линии и найти значения напряженности поля.
Дата добавления: 2015-03-03; просмотров: 604;
