ИСТОЧНИКИ ТОКА 2 страница
2.2. Описание установки и метод измерения
Исследование электростатического поля заключается в нахождении вектора напряженности Е в каждой его точке. Аналитический расчет полей возможен лишь для заряженных тел простой формы (сфера, цилиндр и т.п.). При
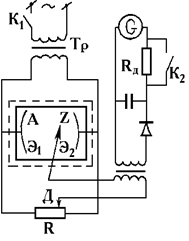 Рис.2.6
Рис.2.6
| сложных поверхностях тел (электродов) такой расчет затруднителен, и тогда электростатическое поле исследуют экспериментально. Для этого сначала определяют положение и форму эквипотенциальных поверхностей, а затем (перпендикулярно к ним) проводят силовые линии. Построение эквипотенциальных поверхностей в полях различной конфигурации производится в данной работе с помощью установки для исследования межэлектродных статистических полей типа ФН9, схематически изображенной на рис.2.6 (упрощенная схема). |
В прямоугольную электролитическую ванну А, заполненную раствором слабого электролита, помещаются металлические электроды Э1 и Э2, поле которых изучается. На зажимы электродов подается переменное напряжение от силового трансформатора Тр.
Между электродами возникает упорядоченное движение зарядов (ионов). При этом плотность тока, согласно закону Ома в дифференциальной форме, в каждой точке электролита пропорциональна вектору напряженности Е в данной точке:
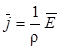 (2.17)
(2.17)
где ρ - удельное сопротивление электролита.
Таким образом, картина линий тока в электролите будет аналогична картине силовых линий Е.
Указанный метод исследования поля называется моделированием. На практике вместо постоянного тока используется переменный ток небольшой частоты, чтобы исключить искажения поля за счет поляризации среды, возникающей в результате электролиза раствора солей.
В измерительную схему входят зонд Z, делитель напряжения R, нулевой гальванометр G с добавочным сопротивлением R9 и тумблером K2.
Зонд Z представляет собой тонкий металлический стержень, хорошо изолированный по всей длине, кроме конца. Измерительная схема работает по следующему принципу: перемещением движка Д на делителе напряжения можно придавать различные значения потенциала (в пределах полной разности потенциалов) этому движку относительно электродов, погруженный в ванну . В какой-нибудь точке поля устанавливается зонд Z. Если зонд находится в такой точке поля, потенциал которой равен потенциалу движка делителя, то не будет тока в цепях зонда и, следовательно, гальванометра. Геометрическое место точек поля, для которых стрелка гальванометра займет нулевое положение при данном положении движка делителя, будет соответствовать одной из эквипотенциальных поверхностей исследуемого поля. Из-за малой глубины ванны в опыте получается не поверхность, а её горизонтальное сечение - линия.
Перемещая движок на делителе напряжения, придают движку различные значения потенциала и для каждого такого значения находят соответствующую эквипотенциальную линию (перемещая зонд в ванне). Фиксирование положения и формы эквипотенциальных линий электростатического поля, получаемых с помощью зонда, производится графически с применением пантографа (рис.2.7).
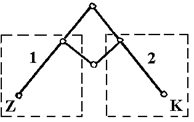 Рис.2.7
Рис.2.7
| К концу направляющей линейки 1 пантографа прикрепляется зонд Z, перемещающийся вместе с линейками в горизонтальной плоскости над ванной. Нижний конец зонда помещен в i электролит, а верхний через первичную обмотку трансформатора гальванометра соединен с движком двигателя напряжения R (см.рис.2.6). Зондом можно обсле- |
довать всю ванну.
Для фиксирования эквипотенциальных линий на листе бумаги, закрепленном на подставке, служит правая часть пантографа. К концу направляющей линейки 2 прикреплен карандаш К. Карандаш может перемещаться вместе с линейкой над листом бумаги, не касаясь её. Прикосновение карандаша к бумаге осуществляется при нажиме на него. Система направляющих линеек устроена так, что любому горизонтальному перемещению зонда в ванне автоматически соответствует перемещению карандаша над листом бумаги.
Найденные с помощью зонда точки, принадлежащие исследуемой эквипотенциальной линии, фиксируются с помощью карандаша на листе бумаги и соединяются плавной кривой.
2.3. Порядок выполнение работы
1. Установить в ванне и закрепить зажимами систему из двух электродов, образующих плоский конденсат.
2. Вложить лист бумаги в крепление подставки пантографа.
3. Обвести зондом контуры поверхностей электродов и получить на листе бумаги соответствующие им эквипотенциальные линии.
4. Тумблер К2 установить в положение "грубо".
5. Включить питание установки, замыкая ключ К1, и зафиксировать положение движка Д.
6. Поместить зонд вблизи одного из электродов.
7. Перемещением движка делителя добиться нулевого положения стрелки гальванометра, только после этого перевести тумблер К2 в положение "точно" (гальванометр при этом приобретает большую чувствительность за счет отключения добавочного сопротивления). Точнее найти положение движка делителя, соответствующее нулевому току гальванометра.
8. Переместить зонд так, чтобы стрелка гальванометра по-прежнему показывала нуль, На листе бумаги зафиксировать не менее 10 точек, принадлежащих исследуемой эквипотенциальной линии.
9. Соединить плавной кривой найденные точки и получить эквипотенциальную линию.
10. Построить четыре эквипотенциальных линии, пользуясь указаниями пунктов 7...9 и помещая зонд на другие точки поля так, чтобы разности потенциалов между двумя соседними линиями были одинаковыми (φ2- φ1= φ3- φ2= φ4- φ3).
11. Установить в ванне новые системы электродов и повторить операции, указанные в пунктах 2...10.
12. Каждое поле построить на отдельном листе, изображая как эквипотенциальные линии, так и построенные ортогонально им силовые линии.
13. На оси симметрии системы электродов (в области поля, где Еx ≠ 0, Еy=0, Еz=0) определить поведение напряженности. Для этого оценить величину напряженности Еx= ∆φ/∆x (В/мм) электрического поля, определив ∆φ - разность потенциалов между соседними эквипотенциальными линиями, ∆x - расстояние между этими линиями вдоль оси симметрии.
14. Оценить точность выполнения измерений.
2.4. Контрольные вопросы
1. Как определяются напряженность и потенциал электростатического поля? Назовите единицы измерения 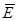 и φ.
и φ.
2. Приведите графики зависимостей Е(r) и φ(r) для точечного заряда.
3. Какая связь существует между 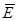 и φ в общем случае и в случае однородного поля?
и φ в общем случае и в случае однородного поля?
4. Как определяются силовые линии и эквипотенциальные поверхности?
5. Какова взаимная ориентация поверхностей равного потенциала и линий напряженности в электрическом поле? Докажите такую ориентацию?
6. Что называется циркуляцией вектора напряженности? Как доказать, что электростатическое поле является потенциальным?
7. Как моделируется и исследуется электростатическое поле в данной работе ?
Литература. [1 §§ 1 - 12; 2 §§ 1- 8; 4 §§ 1, 2, 8] .
3. ОПРЕДЕЛЕНИЕ ЁМКОСТИ КОНДЕНСАТОРА С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО ГАЛЬВАНОМЕТРА
Цель работы: ознакомление с одним из методов измерения емкости конденсатора; экспериментальная проверка формул для определения емкости системы двух конденсаторов, соединенных параллельно и последовательно.
Приборы и принадлежности: баллистический гальванометр, осветитель со шкалой, вольтметр, источник постоянного тока, потенциометр, соединительные провода.
3.1. Теоретические сведения
Заряд q уединенного проводника и его потенциал пропорциональны друг другу:
q = Сφ. (3.1)
Коэффициент С называют емкостью проводника. Единицей измерения емкости в СИ является Фарад: 1 Ф = 1 Кл/1 В.
При наличии вблизи рассматриваемого проводника А другого про- водника В емкость первого возрастает, так как на В под действием поля проводника А происходит перераспределение зарядов: заряды противоположного знака располагаются ближе к А и в целом происходит уменьшение модуля φа. Этот факт используется в специальных устройствах-конденсаторах. Конденсаторы делают в виде двух проводников, расположенных близко друг к другу и называемых обкладками. Обкладкам придают такую форму, чтобы поле, создаваемое находящимися на них зарядами, было сосредоточено внутри конденсатора, при этом внешние тела не влияют на его емкость. Такому условию удовлетворяют две параллельные пластины, два коаксиальных цилиндра, две концентрические сферы. Соответственно бывают плоские, сферические и цилиндрические конденсаторы.
Рассмотрим плоский конденсатор. Пусть q1 и q2 - заряды пластин: q1= -q2; S - площадь каждой пластины; d - расстояние между пластинами. Напряженность поля между обкладками
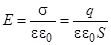 (3.2)
(3.2)
где εо - электрическая постоянная;
ε - диэлектрическая проницаемость среды, заполняющей пространство между пластинами;
σ = q/S - поверхностная плотность зарядов на пластинах.
Разность потенциалов между обкладками (с учетом знаков)
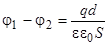 , (3.3)
, (3.3)
где d - расстояние между пластинами.
Таким образом, электрическая емкость плоского конденсатора
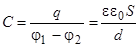 (3.4)
(3.4)
Формула (3.4) емкости плоского конденсатора справедлива только при малых значениях расстояния d между пластинами, когда можно пренебречь нарушениями однородности электростатического поля у краев пластин.
Энергию конденсатора определим следующим образом. Для простоты рассмотрим плоский конденсатор, считая ε =1. На каждую пластину действует сила F = q∙Е = q (σ / 2εо), где q - заряд одной пластины, Е - поле, созданное другой пластиной. При изменении расстояния от 0 до d над конденсатором совершается работа 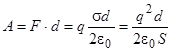
Таким образом, заряженный конденсатор обладает энергией:
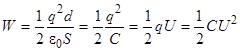 , (3.5)
, (3.5)
или 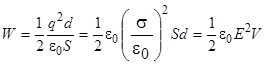 , (3.6)
, (3.6)
где V = Sd - объем, ограниченный конденсатором.
С другой стороны, результатом изменения расстояния между пластинками являются то, что теперь в объеме V = Sd имеется электрическое поле Е. Разумно, поэтому поставить вопрос: где локализована энергия конденсатора - на его пластинах или в пространстве между пластинами (т.е. там, где Е ≠ 0)? Оставаясь в рамках электростатики, ответить на этот вопрос невозможно. Однако исследования переменных полей убедительно показывают, что с электрическим полем действительно связана энергия. При этом в расчете на единицу объема она составит в соответствии с формулой (3.6) величину
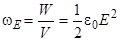 (3.7)
(3.7)
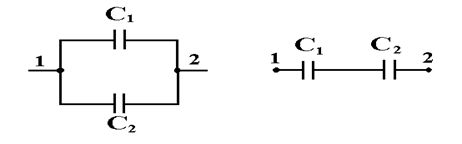
На рис. 3.1 и 3.2 показано параллельное и последовательное соединения конденсаторов, соответственно.
|
Рис.3.1 Рис.3.2
При параллельном соединении напряжение на конденсаторе одинаково: U1 = U2 = U = φ1 - φ2. Общий заряд q = q1 + q2 = C1U + C2U = = (C1 + C2)U = CU. Таким образом, при параллельном соединении общая емкость системы
С = C1 + C2 . (3.8)
При последовательном соединении конденсаторы имеют одинаковый заряд q = q1 = q2. В этом случае очевидно 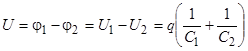 , откуда
, откуда
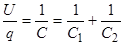 и
и
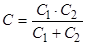 (3.9)
(3.9)
В данной лабораторной работе в основу измерения емкости конденсатора положено соотношение 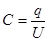 (3.10)
(3.10)
Для измерения q применяется баллистический гальванометр, схематически показанный на рис.3.3.
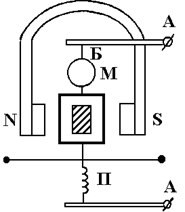 Рис.3.3 Рис.3.3
| Между полюсами постоянного магнита на бронзовой ленточке Б подвешена рамка К, на которую плотно уложены витки измерительной катушки из тонкой проволоки. Бронзовая лента Б одновременно служит токопроводником. Вторым токопроводом является пружина П, свитая из бронзовой ленточки. На нити Б укреплено зеркало М. При прохождении тока через катушку возникает момент сил Ампера, поворачивающий рамку в магнитном поле. Режим работы гальванометра подбирается так, чтобы время прохождения тока через рамку было много мень- |
ше периода собственных (крутильных) колебаний рамки. Для увеличения периода колебаний рамки специально увеличивают ее момент инерции J относительно нити подвеса Б. Время прохождения тока равно в данном случае времени разряда конденсатора через измерительную катушку. Оно сравнимо с величиной τ=RC, где R - сопротивление катушки, С - емкость. Обычно τ не превышает сотых долей секунды. Например, при R = 1000 Ом и С = 1 мкФ величина τ = RС = 10-3 с.
Уравнение движения рамки запишется следующим образом:
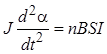 (3.11)
(3.11)
где d2α/dt2 - угловое ускорение, α - угол поворота рамки, n - число витков, В - индукция магнитного поля в воздушном промежутке между полюсами магнита, S - площадь витка, I - сила протекающего по витку тока. Благодаря большому моменту инерции рамка за время разряда конденсатора t практически не успевает выйти из положения равновесия. Поэтому из уравнения движения рамки (3.11) выведем
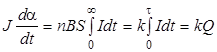 (3.12)
(3.12)
где dα /dt - угловая скорость; k = nBS - коэффициент, зависящий от конструктивных особенностей прибора; Q -заряд, прошедший через рамку. Приобретенная рамкой в момент прохождения тока кинетическая энергия расходуется на работу упругих сил
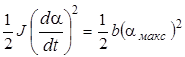 (3.13)
(3.13)
где b - постоянная прибора, αмакс – предельный угол отклонения стрелки гальванометра (угол первого отклонения).
Решая совместно уравнения (3.12) и (3.13), получаем
Q = B α макс, (3.14)
где 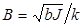 - коэффициент пропорциональности – баллистическая постоянная гальванометра.
- коэффициент пропорциональности – баллистическая постоянная гальванометра.
При этом угол первого отклонения рамки из положения равновесия прямо пропорционален заряду, прошедшему через катушку.
На зеркало З от осветителя падает луч света. Световой зайчик, отражаясь от зеркала, попадает на горизонтальную шкалу.
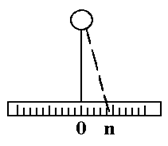 Рис.3.4
Рис.3.4
| При небольших α смещение зайчика по шкале и заряд также пропорциональны (рис.3.4) друг другу Q = В∙ n, (3.15) где n - смещение зайчика в делениях шкалы; В - баллистическая постоянная гальванометра, численно равная заряду, отклоняющему зайчик на 1 деление шкалы. Взяв известную емкость Сo и определив no при |
заданном напряжении Uо, найдем В:
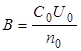 (3.16)
(3.16)
Неизвестную емкость Сx теперь можно определить, задавая U и определяя n:
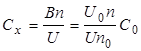 (3.17)
(3.17)
В частности, при U = Uо, Сx= (n/nо)Со.
3.2. Порядок выполнения работы
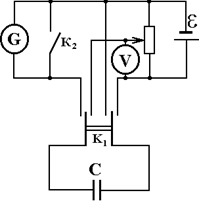 Рис.3.5
Рис.3.5
| 1) Собрать схему, показанную на рис.3.5. Если же установка не требует допол-нительного монтажа, разобраться в схеме и найти на установке все элементы схемы. 2) Определить баллистическую постоянную гальванометра В. Для этого известную емкость Со зарядить до определенного напряжения Uо (произвольно изменяя значения Uo с помощью потенциометра R), затем отключить её от источника и подключить к концам измерительной |
катушки гальванометра G, отсчитывая при этом число делений шкалы nо, на которое отклоняется зайчик из начального положения до конечного при первом отбросе. Переключение конденсатора осуществляется ключом К1. Ключ К2 используется для успокоения гальванометра. Измерения для данного значения Uo повторить 5 раз, найти nоср.
3) Пункт 2 повторить для 4 значений напряжения Uo.
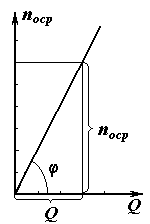 Рис.3.6
Рис.3.6
| 4) Построить график зависимости отклонения зайчика гальванометра nоср от величины заряда Q (Q = СoUo) и по нему, воспользовавшись формулой (3.15), определить В = Q/noср = ctgφ (рис.3.6). 5) Включить вместо емкости Со неизвестную емкость СХ1 (аналогично СХ2) и измерить среднюю величину отклонения зайчика гальванометра nср для неизвестного конденсатора по пункту 2 при напряжении U. 6) Воспользовавшись формулой (3.17), определить емкость СХ1 (аналогично СХ2) СХ1= Вnср/U. 7) Аналогичные измерения провести при параллельном |
и последовательном включениях СХ1 и СХ2. Определить общую емкость в обоих случаях и сравнить их значения со значениями, полученными по формулам (3.8) и (3.9). Образец таблицы для записи результатов измерений находится на рабочем месте.
8) Оценить погрешности измерений.
3.3. Контрольные вопросы
1. Что такое емкость проводника, конденсатора? От чего она зависит? В каких единицах измеряется?
2. Чему равна энергия заряженного конденсатора?
3. Чему равна емкость системы двух конденсаторов при их параллель- ном и последовательном соединениях?
4. Как устроен баллистический гальванометр?
5. Доказать, что предельное отклонение рамки гальванометра пропорционально прошедшему через нее заряду.
6. Как определяется баллистическая постоянная гальванометра?
7. Как работает электрическая схема?
8. Как в данной работе определяется емкость конденсатора?
Литература. [1 §§ 21, 22, 24 - 30; 2 §§ 24 - 30; 4 §§ 9, 10, 12, 13]
4. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ СВОЙСТВ СЕГНЕТОЭЛЕКТРИКОВ
Цель работы: изучение зависимости вектора поляризации Р в сегнетоэлектрике от напряженности Е внешнего электрического поля. Определение зависимости диэлектрической проницаемости ε от Е. Определение коэрцитивной силы и остаточной поляризации.
Приборы и принадлежности: конденсатор ВК-2Б с сегнетоэлектрическим диэлектриком, генератор, осциллограф, два вольтметра.
4.1. Теоретические сведения
Диэлектрики - вещества, которые практически не проводят электрический ток.
Удельное электрическое сопротивление диэлектриков ρ ~ 106-1015 Ом∙м.
Все диэлектрические материалы обладают способностью к электрической поляризации во внешнем электрическом поле.
При этом различают два вида диэлектриков: с неполярными и полярными молекулами.
Электрическое поле, действуя на разноименно заряженные частицы молекул, смещает их в противоположных направлениях, вызывая разделение "центров тяжести" положительных и отрицательных зарядов. В результате молекулы неполярного диэлектрика приобретают электрический дипольный момент.
Электрический диполь - система двух равных по модулю разноименных точечных зарядов (+Q; -Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля.

Рис.4.1
Плечо диполя ī - вектор, направленный по оси диполя от отрица- тельного заряда к положительному и равный расстоянию между ними (рис.4.1)
Дипольный момент 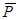 - это вектор, совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо ī:
- это вектор, совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо ī:
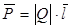 (4.1)
(4.1)
Каждая же молекула полярного диэлектрика имеет определенный дипольный момент в отсутствие электрического поля, но вследствие теплового движения молекулы расположены хаотично и векторная сумма всех дипольных моментов равна нулю. Электрическое поле вызывает частичное упорядочение в расположении диполей, т.е. поляризацию.
Поляризация диэлектрика - явление ориентации диполей или появление под воздействием электрического поля ориентированных по полю диполей.
Для количественного описания поляризации диэлектрика пользуются векторной величиной - вектором поляризации.
Вектор поляризации - дипольный момент единицы объема диэлектрика:
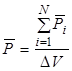 . (4.2)
. (4.2)
Если диэлектрик изотропный, то
P = æ×e0×E (4.3)
где æ - диэлектрическая восприимчивость, характеризующая способность диэлектрика к электрической поляризации;
e0 - электрическая постоянная: e0= 8,85×10-12 Ф/м
Вектор электрического смещения для диэлектрика запишется в виде
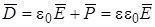 , (4.4)
, (4.4)
где ε - относительная диэлектрическая проницаемость диэлектрика, показы-вающая во сколько раз ослабляется внешнее поле внутри диэлектрика.
Диэлектрическая проницаемость ε связана с диэлектрической восприимчивостью æ равенством
ε = 1 + æ. (4.5)
Внесем в однородное электрическое поле Ео, созданное двумя бесконечными параллельными равномерно заряженными плоскостями, пластинку из однородного диэлектрика (рис.4.2). δ -поверхностная плотность C:\LEXICON\\DOC\HPOLE\сегнето2.pcx 240%, 220% свободных зарядов. δ' -поверхностная плотность, связанных зарядов.
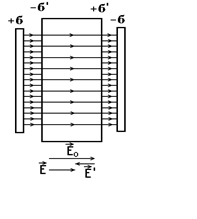 Рис.4.2
Рис.4.2
| Свободные заряды - заряды частиц, способных перемещаться под воздействием электрического поля на макроскопические расстояния. Связанные заряды - заряды, которые входят в состав атомов и молекул, а также заряды ионов в кристаллических диэлектриках с ионной решеткой. Под воздействием поля Ео диэлектрик поляризуется, т.е. происходит смещение зарядов: положительные смещаются по полю, отрицательные - против поля. В результате на грани диэлектрика, обращенной к |
отрицательной плоскости, будет избыток положительных зарядов с поверхностной плотностью +δ', на другой стороне - избыток отрицательных зарядов с поверхностной плотностью -δ' (см.рис.4.2).
Появление связанных зарядов приводит к возникновению дополнительного поля Е', направленного против внешнего поля и ослабляющего его: 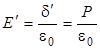 , (4.6)
, (4.6)
Для описания результирующего поля внутри диэлектрика вводится вектор электрического смещения D, характеризующий электрическое поле, создаваемое свободными зарядами, при таком распределении их в пространстве, которое имеется при наличии диэлектрика.
Модуль вектора электрического смещения равен поверхностной плотности свободных зарядов:
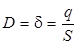 . (4.7)
. (4.7)
Из опыта следует, что для большего класса диэлектриков вектор поляризации Р линейно зависит от напряженности электрического поля Е. Следовательно, диэлектрическая восприимчивость æ - величина постоянная.
У таких диэлектриков электрическая поляризация исчезает после устранения ее причины - внешнего электрического поля.
Сегнетоэлектрики - особый класс диэлектриков, обладающих спонтанной (самопроизвольной) поляризацией, т.е. поляризацией в отсутствии внешнего электрического поля.
К сегнетоэлектрикам относятся, например, детально изученные советскими физиками И.В.Курчатовым и П.П.Кобеко сегнетовая соль NaКС4Н4О6∙4Н2О и титанат бария ВаТiО3.
При отсутствии внешнего электрического поля сегнетоэлектрик представляет собой мозаику из доменов.
Домены - области однородной, спонтанной поляризации (размеры 10-5 ÷ 10-3 см). Они разделены переходной областью (доменная граница) толщиной (10-5÷ 10-7 см).
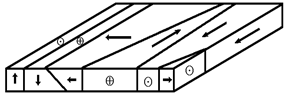
|
Рис.4.3
Схематично доменная структура показана на рис.4.3, где стрелки и знаки  , указывают на направление вектора Р. В смежных доменах направления поляризации различны, поэтому в целом дипольный момент диэлектрика равен нулю. Такое состояние кристалла соответствует минимуму свободной энергии и является термодинамически устойчивым, так как при этом компенсируются электрические поля, создающиеся поверхностными зарядами поляризованных доменов.
, указывают на направление вектора Р. В смежных доменах направления поляризации различны, поэтому в целом дипольный момент диэлектрика равен нулю. Такое состояние кристалла соответствует минимуму свободной энергии и является термодинамически устойчивым, так как при этом компенсируются электрические поля, создающиеся поверхностными зарядами поляризованных доменов.
При внесении сегнетоэлектрика во внешнее электрическое поле происходит переориентация доменов по полю. Связь между вектором поляризации Р и напряженностью Е нелинейная, и, при этом наблюдается явление гистерезиса. Сущность гистерезиса заключается в том, что поляризация сегнетоэлектрика определяется не только значением напряженности поля, но и зависит от предшествовавших состояний поляризации.
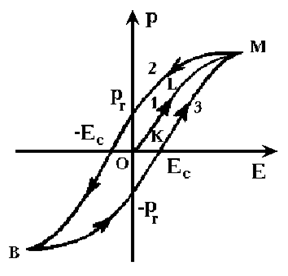 Рис.4.4 Рис.4.4
| На кривой зависимости вектора поляризации от напряженности поля Р = Р (Е) можно выделить три участка (рис.4.4). На участке ОК кривой 1 поляризация линейно зависит от поля и процессы обратимы. При увеличении напряженности электрического поля на втором участке КL кривой Р = Р(Е) процесс переориентации спонтанной поляризации осуществляется путем движения доменных стенок, а также путем образования и прорастания зародышей новых доменов с направлением спонтанной поляризации, близким |
направлению электрического поля. Процессы поляризации становятся необратимыми. При некотором значении Р, соответствующем точке L, кристалл становится однодоменным и достигается насыщение. На участке LМ поляризация снова линейно зависит от поля, увеличение поляризации происходит за счет электронных и ионных смещений.
Если уменьшить напряженность поля, то поляризация кристалла будет уменьшаться не по начальной кривой 1, а по кривой 2, лежащей выше начальной. При Е = О сегнетоэлектрик сохраняет остаточную поляризацию Рr, т.е. сегнетоэлектрик остается поляризованным в отсутствии внешнего электрического поля.
Чтобы уничтожить остаточную поляризацию, надо приложить электрическое поле обратного направления (-Ес).
Величина Ес называется коэрцитивной силой.
Дата добавления: 2015-03-03; просмотров: 1137;
