Понятие закона регулирования. Типовые линейные законы регулирования.
Законом регулирования называют математическую зависимость, в соответствии с которой управляющее воздействие на объект формировалось бы безынерционным регулятором в функции от ошибки системы.
Наиболее часто используют следующие линейные законы регулирования, которые иногда называют типовыми линейными законами регулирования.
Пропорциональный (П-закон), когда управляющее воздействие Ху на объект формируется пропорционально ошибке е:
Ху = Кре;
,
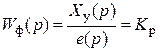где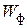 
¾ передаточная функция безынерционного регулятора; Кр ¾ коэффициент передачи регулятора.
Интегральный закон (И‑закон), когда управляющее воздействие на объект формируется пропорционально интегралу ошибки:
;
,
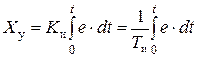где Ти ¾ постоянная интегрирования.
Пропорционально-интегральный закон (ПИ-закон), когда управляющее воздействие на объект формируется пропорционально ошибке и пропорционально интегралу ошибки:
;
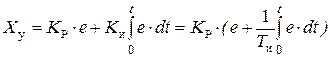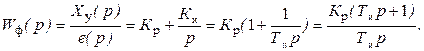
Пропорционально-дифференциальный закон (ПД-закон), когда управляющее воздействие на объект формируется пропорционально ошибке и пропорционально производной ошибки:
,
,
где Тд ¾ постоянная дифференцирования.
Пропорционально-интегрально-дифференциональный закон (ПИД-закон), когда управляющее воздействие на объект формируется пропорционально ошибке, пропорционально интегралу ошибки и пропорционально производной ошибки:
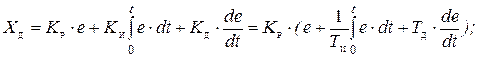
Промышленностью выпускаются регулирующие блоки (регуляторы), которые позволяют реализовать эти законы регулирования (как правило, в приближенном виде).
П-закон обеспечивает хорошее быстродействие, но при статическом объекте управления система работает со статической ошибкой.
И-закон позволяет избавиться от статической ошибки по управляющему воздействию и при статическом объекте от статической ошибки по возмущающему воздействию, но быстродействие системы невысокое.
ПИ-закон сочетает положительные свойства систем с П‑законом и И‑законом, поэтому он обеспечивает хорошее быстродействие и отсутствие статических ошибок.
Введение регулирования по производной в ПД-законе подавляет колебательность, повышает устойчивость, однако не позволяет избавиться полностью от статических ошибок.
ПИД-закон сочетает положительные свойства, обеспечиваемые выше рассмотренными законами. Системы с ПИД‑законом по сравнению с системами с другими типовыми законами обладают повышенным быстродействием, меньшей колебательностью и отсутствием статических ошибок.
Динамические свойства системы при изменении коэффициента передачи регулятора Кр и постоянной интегрирования ТИ изменяются следующим образом (рис. 2.18.1).
При увеличении коэффициента Кр быстродействие системы сначала увеличивается, затем уменьшается за счет увеличения колебательности. Колебательность и перерегулирование увеличиваются с увеличением Кр. При больших Кр система становится неустойчивой.
Такой же характер носит изменение динамических качеств системы при увеличении коэффициента передачи КИ (уменьшение постоянной интегрирования ТИ).
Значения Кр и ТИ, при которых начинается уменьшение быстродействия, а затем система становится неустойчивой, зависят от динамических свойств системы в целом.
Введение дифференциальной составляющей в закон регулирования позволяет подавить колебательность и, следовательно, увеличить допустимые значения Кр и ТИ, увеличить быстродействие. Для систем с ПД-законом дифференциальная составляющая позволяет снизить статическую ошибку за счет увеличения допустимых значений Кр по перерегулированию, колебательности и запасу устойчивости. Однако чрезмерное увеличение постоянной дифференцирования ТД приводит к снижению быстродействия.
 |
Рис. 2.18.1 Переходные процессы системы с различными коэффициентами передачи
и постоянными интегрирования
Таким образом, задача синтеза системы автоматического регулирования с заданными показателями качества может быть решена путем выбора закона регулирования и подбора коэффициента передачи Кр и постоянных интегрирования и дифференцирования ТИ и ТД , например путем моделирования на ЭВМ.
Дата добавления: 2015-02-28; просмотров: 3922;