Типовое гармоническое воздействие. Частотные характеристики систем и звеньев.
Гармоническое воздействие :
x = Ахsinwt,
где Ах ¾ амплитуда; w¾ угловая частота.
Если на линейную систему или звено подать гарм-кие возд-вия, то на выходе также будет гармонический сигнал:
y = Аysin(wt+φ).
Амплитуда Аy будет зависеть от частоты входного сигнала, и разность фаз между входным и выходным сигналами будет зависеть от частоты входного сигнала. Таковы физические свойства систем и линейных звеньев.
Реакция системы (звена) на гармоническое воздействие характеризуется его частотными характеристиками.
Амплитудно-частотной характеристикой (АЧХ) называется зависимость отношения амплитуд выходного и входного гармонических сигналов от частоты в установившемся режиме:
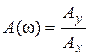 .
.
Первый рисунок ниже
Где К- коэфф. передачи звена
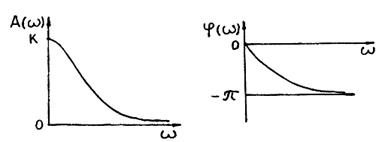
Фазово-частотной характеристикой (ФЧХ) называется зависимость разности фаз j(w) между входным и выходным сигналами от частоты в установившемся режиме.
Возможный вид графиков АЧХ и ФЧХ
 |
Частотная передаточная функция является комплексной функцией, поэтому:
W(jw) =Y(jw)/X(jw) = U(w) + jV(w) = A(w) e jj(w) .
где U(w) – действительная часть; V(w) – мнимая часть; A(w)- модуль функции; j(w) – аргумент функции
A(w)= под корнем U2(w)+V2(w)
j(w) = arctg V(w)/U(w)
Кроме того, строится совместная амплитудно-фазовая частотная характеристика (АФЧХ) в координатах U(w) и jV(w):
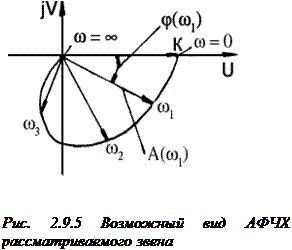 |
График АЧХ, построенный в логарифмическом масштабе, называют логарифмической амплитудной характеристикой (ЛАХ), график ФЧХ, построенный в логарифмическом масштабе, называют логарифмической фазовой характеристикой (ЛФХ).
Перевод значений АЧХ в значения ЛАХ осуществляется следующим образом:
L(w) = 20 lgA(w), дБ.
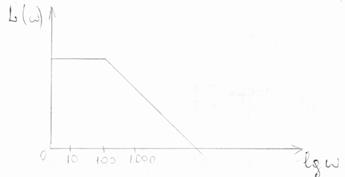
Единицей измерения логарф-ой амплитуды является децибел, а частоты – декада (дек), что соответствует увеличению частоты в 10 раз.
Дата добавления: 2015-02-28; просмотров: 2214;
