Типовые ступенчатые и импульсные воздействия. Временные характеристики систем и звеньев.

Все системные звенья работают при каких-то воздействиях. Для того, чтобы анулировать эти воздействия при анализе и синтезе систем, ввели понятие «типовые воздействия», которые являются приблизительным теоретическим описанием наиболее часто встречающихся реальных возд-вий.

В качестве типовых используют следующие воздействия.

Ступенчатое воздействие:

0 при t < 0;

x(t)=

1(t)*а при t ³ 0 ,

где 1(t) ¾ единичное ступенчатое воздействие; а - величина ступенчатого воздействия.

Реакция системы или звена на един-ое ступ-ое возд-вие называется переходной функцией.

Возможный вид переходных функций

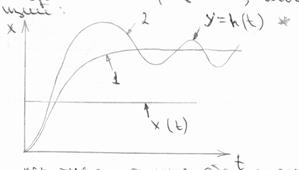
Обычная переходная функция обозначается h(t).

Переходные функции вида 1 называются периодическими, а вида 2 – колебательными.

Импульсное воздействие (дельта-функция):

¥ при t = 0;

x(t) = d(t) =

0 при t « 0.

d(t) имитирует короткое импульсное воздействие

.

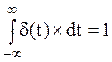d(t) является производной единичной ступенчатой функции:

d(t) = 1^I(t).

Реакция системы или звена на d(t) называется импульсной переходной функцией (функцией веса).

Возможный вид импульсных переходных функций

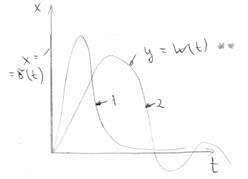
Обычная импульсная переходная функция обозначается W(t).

Переходная и импульсная функции называются временными характеристиками системы или звена.

Из выражений (*) и (**) следует взаимосвязь между переходной и импульсной переходной функциями:

W(t) = h'(t);

.

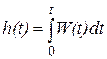Учитывая, что изображение Лапласа имеет вид L[w(t)]=1, следует взаимосвязь между импульсной переходной функцией, переходной функцией и передаточной функцией системы или звена:

L[w(t)]=w(p);

w (t)=L^-1[w(p)];

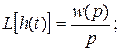
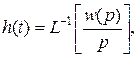
где L ¾ прямое преобразование Лапласа; L^-1 ¾ обратное преобразование Лапласа.