Культура и искусство Нововавилонского царства
Для нововавилонской архитектуры характерно соблюдение старых традиций зодчества Двуречья: белёные глухие наружные стены храмов и дворцов расчленялись только чередованием ниш и выступов. Все строения возводились всё также из сырцового кирпича.
Величественным памятником культуры Нововавилонского царства является сам город Вавилон, раскопанный археологами. Вокруг Вавилона на некотором расстоянии была возведена стена, внутри которой могло скрываться в случае военных действий окрестное население. Собственно город, имевший несколько сот тысяч жителей, был обнесён двойной кирпичной стеной исключительной высоты и мощности, со рвом и валом перед нею. Город пересекался Евфратом, через который был перекинут мост на каменных быках. Центром городских укреплений была цитадель,которая представляла собой комплекс дворцов и расположенная частично внутри, частично снаружи собственно города. Весь город прорезала прямая “прецессионная дорога”, мощёная посередине плитами белого и розового камня. Эта дорога вступала в пределы города через северные ворота, посвящённые богине Иштар. Ворота эти были покрыты синими изразцами с рельефными цветными рядами изображений быков и мифических чудовищ. Дорога вела далее вдоль стен цитадели к стенам ограды храма Мардука. Посреди этой ограды высилась 90-метровая громада храмовой ступенчатой башни “Этеменанки” (вошедшей в легенду под названием “Вавилонской башни”). Подобные башни (зиккураты) составляли непременную часть храма главного бога любого вавилонского города и строились в три этажа, отражая мифические представления о построении мироздания (небо, земля и подземные воды), или в семь этажей—возможно, в честь семи астральных божеств. Башня “Этеменанки” состояла из семи разноцветных этажей и была увенчана синим храмиком с золочёными рогами по углам; здесь находилась золотая статуя Мардука.
Библейская легенда, согласно которой бог наказал людей за дерзкую попытку построить башню “высотой до неба” тем, что создал различие в языках, содержит осуждение пленёнными иудеями строительных работ в храмах, которые проводились Навуходоносором II. В этой легенде содержится также попытка по-своему объяснить существовавшее уже тогда многоязычие населения этого важнейшего экономического, политического и культурного центра Ближнего Востока.[189]
 Рис. 34. Вавилонская глиняная табличка, содержащая геометрические задачи// http://znanie.podelise.ru/docs/89846/index-2835-4.html
Рис. 34. Вавилонская глиняная табличка, содержащая геометрические задачи// http://znanie.podelise.ru/docs/89846/index-2835-4.html
Изобразительное искусство нововавилонского периода находилось в зависимости от ассирийского; но характерная для последнего тематика прославления царских побед и войска была в Вавилоне исключена; здесь изразцовые рельефы и плоские фризы на башнях ворот и стенах дворцов содержали только сухое орнаментальное воспроизведение фигур священных животных, а в камнерезном искусстве встречаются лишь сцены поклонения различным символам божеств. Своей техникой и композиционными приёмами нововавилонское искусство сыграло большую роль в сложении искусства Передней Азии времён персидского владычества.
Датировка отдельных памятников вавилонской литературы до сих пор представляет очень трудную задачу, и нельзя сказать с уверенностью, какие её произведения можно отнести к нововавилонскому периоду. Во всяком случае в нововавилонский период усердно копировались и переписывались памятники древней письменности. Самостоятельно развивалась астрономия, оказавшая немалое влияние на греческую науку. Вавилонская культура, наука, литература, искусство надолго пережили падение Вавилонского царства и явились важной составной частью древней культуры человечества.[190]

Рис. 35. Вавилонские цифры// http://lib.znate.ru/docs/index-30828.html?page=3
Математическое наследие древнего Вавилона... Это название обычно распространяется на совокупность государств, располагавшихся в междуречье Тигра и Евфрата и существовавших в период от 2000 до 200 г. до н. э. Вавилоняне писали клинописными значками на глиняных табличках, которые в немалом количестве дошли и до наших дней (более 500000, около 400 из них связаны с математикой). Поэтому-то мы и имеем довольно-таки полное представление о математических достижениях учёных Вавилонского государства. Важно также здесь отметить, что корни культуры вавилонян были в значительной степени унаследованы от шумеров,а именно- клинописное письмо, счётная методика и т. п. Вавилонские математические тексты носят преимущественно учебный характер. Из них нам видно, что вавилонская расчётная техника была намного совершеннее египетской, а круг решаемых задач был существенно шире. Есть задачи на решение уравнений второй степени, геометрические прогрессии. При решении ,несомненно,применялись пропорции, средние арифметические и проценты. Методы работы с прогрессиями были намного глубже, чем у египтян. Линейные и квадратные уравнения решались ещё в эпоху Хаммурапи,при этом использовалась геометрическая терминология (произведение ab называлось площадью, abc — объёмом, и т.д.). Многие значки для одночленов были шумерскими, из чего можно сделать вывод о древности этих алгоритмов.И эти значки употреблялись, как буквенные обозначения неизвестных в нашей алгебре. Встречаются также как кубические уравнения, так и системы линейных уравнений. Венцом планиметрии была теорема Пифагора. Как и в египетских текстах, излагается только алгоритм решения (на конкретных примерах), без комментариев и доказательств. Но анализ алгоритмов показывает, что общая математическая теория у вавилонян , конечно, была.
Шумеры и вавилоняне использовали 60-ричную позиционную систему счисления, увековеченную в нашем делении круга на 360°, часа на 60 минут и минуты на 60 секунд. Они писали, как и мы сейчас, слева направо. Однако запись необходимых 60 цифр была своеобразной. Значков для цифр было всего два, обозначим их Е (единицы) и Д (десятки). Позже появился значок для нуля. Цифры от 1 до 9 изображались как Е, ЕЕ, … ЕЕЕЕЕЕЕЕЕ. Далее шли Д, ДЕ, … ДДДДДЕЕЕЕЕЕЕЕЕ (59). Таким образом, число изображалось в позиционной 60-ричной системе, а его 60-ричные цифры — в аддитивной десятичной. Аналогично записывались и дроби. Для популярных дробей 1/2, 1/3 и 2/3 также были специальные значки.В современной научной литературе для удобства используется компактная запись вавилонского числа, например:
4,2,10; 46,52 расшифровывается эта запись следующим образом: 4 × 3600 + 2 × 60 + 10 + 46/60 + 52/3600.Для умножения применялся громоздкий комплект таблиц, отдельно для умножения на 1-20, 30…50. Деление m/n они заменяли умножением m ×(1/n). Для нахождения 1/n у них были специальные таблицы. Другие таблицы помогали возводить в степень, извлекать корни и даже находить показатель степени n, если дано число вида 2n (эти двоичные логарифмы использовались для подсчёта процентов по кредиту). Без многопудовой библиотеки таблиц никакие расчёты в Вавилоне были невозможны.
Для вычисления квадратных корней вавилоняне изобрели итерационный процесс: новое приближение получалось из предыдущего по формуле метода Ньютона:an + 1 = (an + N / an) / 2.[191]
 Рис. 36. Вавилонская табличка с вычислением
Рис. 36. Вавилонская табличка с вычислением 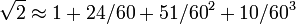
= 1.41421296...// http://portfele.ru/docs/168/index-86034.html
Геoметрические знания вавилонян, наверное, превышали египетские, так как в текстах помимо общих типов задач встречаются начатки измерения углов и тригонометрических соотношений. В основном, впрочем, они тоже состояли из вычислений площадей и объемов прямолинейных фигур, обычных для элементарной геометрии. Имелись и способы приблизительного вычисления объемов, основанные на своеобразном усреднении размеров.В геометрии рассматривались те же фигуры, что и в Египте, плюс сегмент круга и усечённый конус. В ранних документах полагают,что π = 3.Но чуть позже встречается приближение 25/8 = 3,125. Встречается также и необычное правило: площадь круга есть 1/12 от квадрата длины окружности, т.е. π2R2 / 3. Ещё при Хаммурапи впервые появляется теорема Пифагора, причём в общем виде.Эта теорема снабжалась особыми таблицами и широко применялась при решении разных задач. Также вавилоняне умели вычислять площади правильных многоугольников,вероятно, им был знаком принцип подобия. Для площади неправильных четырёхугольников использовалась та же приближённая формула, что и в Египте.Всё же богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приёмов, лишённых доказательной базы. Систематический доказательный подход в математике появился только у греков.[192]
Можно сказать,что вавилонcкая культура – это одна из древнейших культур на земном шаре ,она восходит своими корнями к IV тысячелетию до н. э. Древнейшими очагами этой культуры были города Шумера и Аккада, а также Элама, издавна связанного с Двуречьем. Вавилонская культура оказала большое влияние на развитие древних народов Передней Азии и античного мира. Одним из наиболее значительных достижений шумерийского народа было изобретение письменности, появившейся в середине IV тысячелетия до н.э. Именно письменность позволила установить связь не только между современниками, но даже между людьми различных поколений, а также передать потомству важнейшие достижения культуры. Развитие хозяйственной жизни, главным образом земледелия, приводило к необходимости установления календарных систем, которые возникли уже в шумерийскую эпоху. Для создания календаря необходимо было иметь некоторые знания в области астрономии. Древнейшие обсерватории устраивались обычно на верхней площадке храмовых башен (зиккуратов), развалины которых были найдены в Уре, Уруке и Ниппуре. Вавилонские жрецы умели отличать звезды от планет, которым были даны особые названия. Сохранились перечни звезд, которые были распределены по отдельным созвездиям. Была установлена эклиптика (годичный путь Солнца по небесной сфере), которую разделили на 12 частей и соответственно на 12 зодиакальных созвездий, многие названия которых (Рак, Скорпион, Лев, Весы,Козерог и т.д..) сохранились до наших дней. В различных документах регистрировали наблюдения над планетами, звездами, кометами, метеорами, солнечными и лунными затмениями.
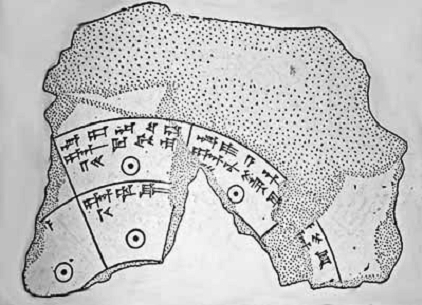 Рис. 37. Фрагмент вавилонской астролябии// http://my.mail.ru/community/catastrof/1C0CDE70DC2F3E39.html
Рис. 37. Фрагмент вавилонской астролябии// http://my.mail.ru/community/catastrof/1C0CDE70DC2F3E39.html
О значительном развитии астрономии говорят данные, фиксирующие моменты восхода, захода и кульминации различных звезд, а также умение вычислять промежутки времени, их разделяющие. В VIII–VI вв. вaвилонские жрецы и астрономы накопили большое количество знаний, имели представление о процессии (предварения равноденствий) и даже могли предсказывать затмения. Некоторые наблюдения и знания в области астрономии позволили построить особый календарь, отчасти основанный на лунных фазах. Основными календарными единицами счета времени были сутки, лунный месяц и год. Сутки делились на три стража ночи и три стража дня. Одновременно с этим сутки делились на 12 часов, а час делился на 30 минут, что соответствует шестеричной системе счисления, лежавшей в основе вавилонской математики, астрономии и календаря. И в календаре отразилось стремление разделить сутки, год и круг на 12 больших и 360 малых частей.
Начало каждого лунного месяца и его продолжительность определялись каждый раз специальными астрономическими наблюдениями, ведь начало каждого месяца должно было совпадать с новолунием. Различие между календарным и тропическим годом исправлялось при помощи вставочного месяца, что устанавливалось распоряжением государственной власти.[193]
Примерные тесты по теме:
1."Вавилонскую и халдейскую историю" с "допотопных" времен до смерти Александра Македонского написал
а)Берос
б)Иосиф
в)Евсевий
г)Геродот
2.Основателем Нововавилонского царства был
а)Набонид
б)Набопаласар
в)Навуходоносор II
г)Киаксар
3.Какой год принято считать началом Нововавилонского царства
а)628 г. до н.э.
б) 626 г. до н.э.
в) 614 г. до н.э.
г) 609 г. до н.э.
4. Навуходоносор II умер в
а)562 г. до н.э.
б)585 г. до н.э.
в) 593 г. до н.э.
г) 598 г. до н.э.
5. Навуходоносор впервые занял Иерусалим в
а) 597 г. до н.э.
б) 590 г. до н.э.
в) 587 г. до н.э.
г) 586 г. до н.э.
6.В борьбе с Тиром дело окончилось
а)миром
б)компромиссом
в)разгромом города
г)недовольством граждан
7.Все чиновники государственного аппарата получали жалованье от царя
а)натурой
б)серебром
в)золотом
г)либо натурой,либо серебром
8.Сыном Навуходоносора II был
а)Авельмардук
б)Лабашимардук
в)Набонид
г)Нериглиссар
9. Верховным божеством жителей финикийского города Тира, славных мореплавателей, чьим именем они назвали Гибралтар, был
| а) | Мелькарт |
| б) | Мардук |
| в) | Энлиль |
| г) | Гильгамеш |
10. Одними из первых в мировой истории военного искусства ассирийцы стали использовать
| а) | пехотинцев |
| б) | лучников |
| в) | конницу |
| г) | боевые колесницы |
11.Шумеры и вавилоняне использовали ... позиционную систему счисления
а)20-ричную
б) 40-ричную
в) 50-ричную
г)60-ричную
12.В математике вавилонян значков для цифр было
а)2
б)3
в)4
г)5
13.Самый великолепный храм Вавилонии
а)зиккурат
б)храм Амона
в)ковчег
г)храм,построенный Соломоном
14. Крупнейшая библиотека, состоявшая из сотен тысяч глиняных табличек, была создана в столице Ассирии
| а) | Фивах | ||||||||
| б) | Библе | ||||||||
| в) | Хаттуше | ||||||||
| г) | Ниневии 15. «Столбами Мелькарта», верховного бога жителей Тира, финикийцы назвали пролив
|
Ключ
А
Б
Б
А
А
Б
Г
А
А
В
Г
А
А
Г
В
Список использованной литературы
1. Бадак А.Н. ,Войнич, И.Е.,Волчек Н.М .и др. Т.3. Век железа. Всемирная история: В 24 т. , Мн.: "Литература", 1998 г. Гл. 4
2. Белявский ,В.А. Вавилон легендарный и Вавилон исторический - М.: "Мысль", 1971 .- 319 с.
3. Бонгард-Левин, Г.М. Древние цивилизации. Под общей ред. Г.М.Бонгард-Левина. М.:" Мысль". 1989.-478c.
4. Вигасин ,А.А. ,Дандамаев, М.А. ,Крюков ,М.В. История Древнего Востока: Учебник для студентов вузов, обучающихся по специальности «История» (под ред. Кузищина В.И.) Изд. 3-е, перераб., доп. М.: "Высшая школа",2003.- 462 с.
5. Дандамаев ,М.А., Виноградов ,И.В. Нововавилонская держава и поздний Египет./История Древнего мира. Расцвет Древних обществ.- М.:"Знание", 1983 .-572 с.
6. Дьяконова, И.М. , Неронова , В. Д,. Свенцицкая, И.С. История Древнего Мира т.2. Расцвет Древних обществ: в 3-ех т., Издание второе/Ред. И.М. Дьяконова, В. Д. Нероновой, И.С. Свенцицкой - М.: «Наука», 1983.-524c.
7. Редер,Д.Г.,Черкасова Е.А. История древнего мира.Ч I.Первобытное общество и Древний Восток.Учебное пособие для студентов ист.фак.пединститутов /Под ред.Ю.С.Крушкол.-2-е изд.,испр. и доп.-М.:"Просвещение",1979.-288 с.
8. Рыбников ,К. А. История математики: учебник. – М.: "МГУ", 1994. – 496с.
9. Стройк, Д. Я . Краткий очерк истории математики. – М.: "Наука", 1990. – 251с.
10. Тураев, Б.А. История древнего Востока. Том 2 \Под редакцией В.В. Струве и И.Л Снегирева. - Ленинград: "Социально-экономическое", 1935.-322c
11. История Востока; «Восточная литература» РАН, Москва, 1997. Гл. 15
Дата добавления: 2015-02-28; просмотров: 7591;
