Капиллярные явления при пайке

Капиллярные явления играют в пайке исключительно большую роль. От того, насколько хорошо расплавленный припой смачивает поверхность основного металла, и затекает в зазоры, в конечном итоге зависит получение плотного и прочного паяного соединения.

Согласно статической теории, растекание жидкостей и смачивание ими поверхности твердого тела сопровождается увеличением поверхности и происходит в результате работы сил поверхностного натяжения. Эта работа совершается разностью давлений между вогнутой и выпуклой стороной поверхности смачивающей жидкости и может быть определена, исходя из изменения энергии этой поверхности.

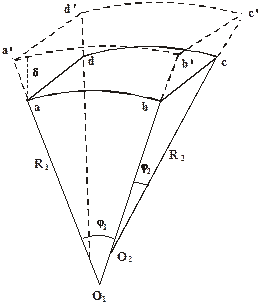
Рассмотрим условия равновесия элементарного криволинейного элемента – abcd.

Пусть нормали в точках а и b элемента рассматриваемой поверхности пересекаются в точке О₁, образуя угол w₁, а нормали в точках b и с пересекаются в точке О₂, образуя угол w₂. Тогда площадь прямо-угольного элемента аbсd будет равна произведению сторон S = аb∙bс.

Под действием разности давлений между вогнутой и выпуклой стороны поверхности элемента точки а, в, с и dпереместятся по нормалям на расстояние d соответственно в положение а', в', с', d', образуя элементы с площадью S₁. Площадь нового элемента через углы w₁ и w₂ будет равна

,

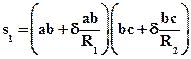где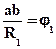

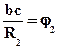
Пренебрегая малыми величинами второго порядка, получим

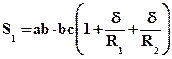(18)

Приращение поверхности рассматриваемого элемента жидкости при перемещении составит

,

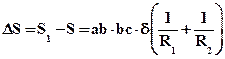тогда работа преодоления сил поверхностного натяжения равна

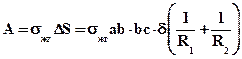
С другой стороны, эта работа может быть выражена через разность давлений между вогнутой и выпуклой стороной поверхности рассматриваемого элемента

А = (Р₁ – Р₂)∙аb∙bс∙d,

где Р₁– давление с вогнутой стороны;

Р₂ – давление с выпуклой стороны.

Никакие другие силы, кроме сил молекулярного взаимодействия, в увеличении поверхности жидкости не участвуют, поэтому оба выражения можно приравнять

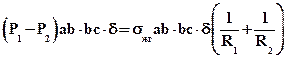
откуда

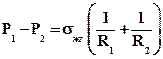(19)

Данное выражение является первым уравнением капиллярности (формула Лапласа). Из него следует, что поверхностный слой жидкости, имеющий кривизну, испытывает добавочное давление по сравнение с тем, которое он испытывает при наличии плоской поверхности. Этим добавочным давлением главным образом обусловлены все капиллярные явления.

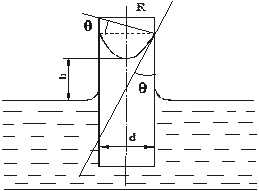
Рис. 8 – Схема подъема жидкости в капилляре

Например, если жидкость течет по капилляру диаметром d, то высота его поднятия над заданным уровнем поверхности ванны, согласно закону капиллярности будет определяться разностью давлений между вогнутой и выпуклой стороной поверхности мениска. Избыточное давление Р₁ – Р₂ может быть выражено через высоту столба жидкости над заданным уровнем и его плотность.

При малом диаметре капилляра свободная поверхность жидкости будет иметь форму сферы, тогда

,

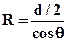где q – краевой угол.

Подставив полученные значения радиуса мениска в выведенное уравнение, получим

,

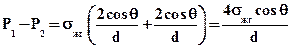но разность давлений будет уравновешиваться столбом жидкости высотой h, тогда

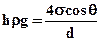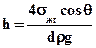, или (20)

где r – плотность жидкости.

Следовательно, высота поднятия жидкости в капилляре пропорциональна ее поверхностному натяжению и смачивающей способности, и обратно пропорциональна диаметру капилляра и плотности жидкости.

В случае капиллярного течения жидкости между двумя параллельными пластинками высота подъема определяется из тех же соотношений. Если принять расстояние между пластинами равными а и малым, а ширина пластин достаточно велика, то поверхность жидкости в зазоре примет форму цилиндра, для которого

,

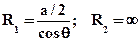тогда высота подъема жидкости определится:

.

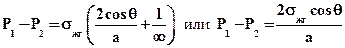Также как и в предыдущем случае, высота подъема h определится

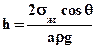(21)

Таким образом, высота капиллярного поднятия жидкости в зазоре между двумя параллельными пластинами в два раза меньше, чем в капилляре круглого сечения.

Поскольку в процессе пайки припои находятся в жидком состоянии, то на них можно распространить полученные уравнения. Однако при этом необходимо иметь в виду, что уравнение выведены для случая не взаимодействующих с твердым телом жидкостей. В процессе же пайки происходит активное взаимодействие в контакте расплавленный припой – основной металл; поэтому капиллярные явления, протекающие в условиях пайки более сложны, и не вполне точно описываются выведенными уравнениями.

ЛЕКЦИЯ №3