Показатели изменчивости метеорологических характеристик.

При проектировании, строительстве и эксплуатации дорог приходится решать различные задачи с учетом климатических показателей, которые можно разбить на три группы:

1. Показатели временной структуры – периодичные изменения элемента во времени, т.е. суточные, декадные, месячные и годовые изменения параметров, характеризующиеся амплитудой и моментом наступления экстремальных и других значений элементов (средними данными и повторяемостью).

2. Показатели непериодичных изменений элемента, связанности рядов между собой, межсуточной изменчивости, непрерывной продолжительности значений элемента выше или ниже заданного уровня – коэффициент корреляции (корреляция - от позднелат. correlatio – соотношение или взаимозависимость между соседними членами ряда); среднее значение межсуточных изменений; среднее квадратичное отклонение межсуточных изменений; средняя непрерывная продолжительность значений элемента выше или ниже некоторого заданного значения (уровня); число периодов непрерывной продолжительности значений элемента выше (ниже) заданного уровня; повторяемость и накопленная повторяемость различных значений непрерывной продолжительности выше (ниже) заданного уровня.

3. Показатели комплексной оценки метеорологических элементов – повторяемость и накопленная повторяемость сочетаний значений комплексирующих элементов; коэффициент корреляции между значениями комплексирующих элементов (чем ближе к 1 коэффициент корреляции – тем плотнее взаимосвязь или соотношение); корреляционное отношение. КОРРЕЛЯЦИЯ в математической статистике, вероятностная или статистич. зависимость, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной, корреляц. зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или же когда среди условий, от к-рых зависят и тот и другой признаки, имеются общие для них обоих условия. Пример такого рода зависимости даёт корреляционная таблица. Из табл. видно, что при увеличении высоты сосен в среднем растёт и диаметр их стволов; однако сосны заданной высоты (напр., 23 м) имеют распределение диаметров с довольно большим рассеянием. Если в среднем 23-метровые сосны толще 22-метровых, то для отд. сосен это соотношение может заметным образом нарушаться. Статистическая Корреляция в обследованной конечной совокупности наиболее интересна тогда, когда она указывает на существование закономерной связи между изучаемыми явлениями. РЕГРЕССИЯ в теории вероятностей и математической статистике - это зависимость среднего значения к.-л. величины от нек-рой другой величины или от нескольких величин. В отличие от чисто функциональной зависимости у = f (х), когда каждому значению независимой переменной х соответствует одноопределённое значение величины у, при регрессионной связи одному и тому же значению х могут соответствовать в зависимости от случая различные значения величины у.

Все основные метеорологические показатели имеют вероятностную природу, т.е. могут быть предсказаны только с каким-то процентом вероятности, и, поэтому, при их определении используются методы математической статистики и, в частности, устанавливаются:

- повторяемость различных значений элемента;

- накопленная повторяемость (обеспеченность);

- среднее арифметическое значение;

- крайние (максимальное, минимальное) значения;

- показатели изменчивости;

- показатели асимметрии и крутости кривой распределения.

Повторяемость – отношение числа случаев со значениями рассматриваемого метеорологического элемента, входящих в данную градацию (интервал), к общему числу членов ряда. Выражается в долях единицы или в процентах. Суммарную повторяемость, полученную на основании длинного ряда наблюдений, называют интегральной вероятностью, или обеспеченностью.

Накопленная повторяемость – отношение суммарного числа случаев, входящих в градации рассматриваемого участка статистического ряда (до и после определенной величины), к общему числу членов ряда. Ее можно определить последовательным суммированием относительных или средних абсолютных частот соответствующих интервалов в ряду статистического распределения.

Среднее арифметическое значение – отношение суммы значений членов ряда к общему их числу. В качестве дополнительных показателей среднего значения применяются медиана – значение среднего члена в ряду значений простого ранжированного распределения, и мода – значение, наиболее часто встречающееся в ряду метеорологических измерений.

Крайние значения – предельные показатели метеорологических элементов, зафиксированные в определенный период времени в рассматриваемом географическом пункте. Крайние значения климатических параметров (абсолютная минимальная и абсолютная максимальная температура воздуха, суточный максимум осадков) характеризуют те пределы, в которых заключены значения климатических параметров. Эти характеристики выбирались из экстремальных за сутки наблюдений. Различают абсолютный максимум или минимум, среднее из максимальных или минимальных значений и максимум или минимум заданной обеспеченности.

Показатели изменчивости – расчетные характеристики, с помощью которых оценивается степень рассеивания значений исследуемого элемента по отношению к его среднеарифметическому значению. К показателям изменчивости относятся:

1. Среднеквадратическое отклонение:

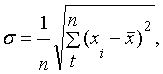
где n – число наблюдений;

х_i– значение при t-м наблюдении;

х – средняя арифметическая величина (х₁+х₂+…х_n/n).

2. Коэффициент вариации (от лат. variatio - изменение):

.

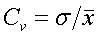3. Дисперсия (от лат. dispersio - рассеяние),в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т. е. отклонения от среднего. В статистическом понимании Дисперсия есть среднее арифметическое из квадратов отклонений величин Хi от их среднего арифметического. В теории вероятностей Дисперсией случайной величины X называется математическое ожидание М(Х - а)² квадрата отклонения случайной величины X от её математического ожидания, а – некоторое число, характеризующее случайную величину, а>0. МХ = а. Математическое ожидание MX для непрерывной случайной величины находится через интеграл х f(x)dx.

х = σ².