Кількісні показники надійності.

Імовірність безвідмовної роботи P(t) на протязі часу (напрацювання) (і) визначають із виразу:

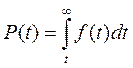
де f(t) - густина розподілення часу безвідмовної роботи. При невідомих значеннях f(t), P(t) визначають по статистичним даним про відмови:

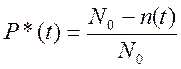
де P*(t) - статистична оцінка ІБР;

No- число виробів на початку випробувань;

n(t)- число деталей, які відмовили за час (t).

При великій кількості виробів No статистична оцінка P*(t) практично збігається з імовірністю P(t).

В якості прикладу можна розглянути розподілення Вейбула, для якого густина розподілення f(t) задається виразом:

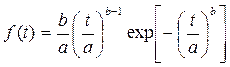
де "а" і "в" параметри розподілення. Для цього розподілення вірогідність безвідмовної роботи :

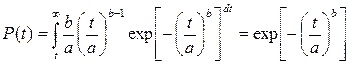
Середнє напрацьовування до відмови для виробів, які неможливо ремонтувати:

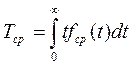
Де fср- густина розподілення напрацювання до відмови. Приблизно середнє напрацювання до відмови визначають по формулі:

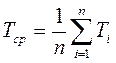
де Ті- час напрацювання до відмови;

і- вироби в партії із

п - виробів.

Із розподілення Вейбула

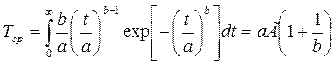
Де 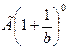- γ – функція

Напрацювання на відмову, якщо вона виражена в одиницях часу, уявляє собою середній час безвідмовної роботи. Визначення цього показника для виробів, які підлягають і не підлягають ремонту вимагає введення понять інтенсивності відмов λ(t) і параметру потоку відмов ω(t) (інтенсивності потоку відмов для виробів, які ремонтуються). Інтенсивність відмов для виробів, які не підлягають ремонту:

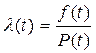
Фізичний зміст визначення розкривається наближеною формулою:

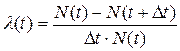
При достатньо малому Δt

Наприклад, у випадку розподілення Вейбула:

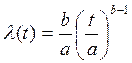
А при експоненціальному розподіленні, якщо b = 1

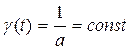
Інтенсивність відмов є параметром, тісно пов’язаним з імовірністю безвідмовної роботи:

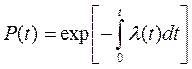
Для виробів, які ремонтуються, середня кількість відмов mcp(t) до напрацювання (t) при випробовуванні n – виробів визначають по формулі:

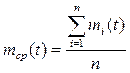
де mi- число відмов і-ro виробу. Гранична величина mcp(t) уявляє собою математичне очікування числа відмов до напрацювання (t):

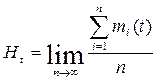
Параметр потоку відмов ω(f), який характеризує інтенсивність потоку відмов виробів, які ремонтуються, визначають із виразу:

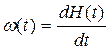
Або наближено:

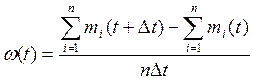
де Δt - достатньо малий проміжок часу. Вводячи ці параметри, можна визначити середнє напрацювання до першої відмови для виробів, які ремонтуються, при пуасонівському потоці відмов:

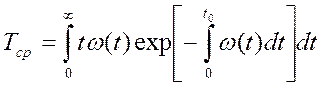
І напрацювання на відміну Т, в інтервалі напрацювань від t1 до t2

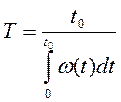
Зміст останнього виразу найбільш ясний із формули напрацювання на відмову для кінцевої сукупності (партії) виробів:

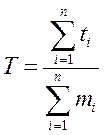
Кількісний показник тривалості – γ – процентний ресурс Трγ – можна визначити із виразу:

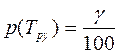
Де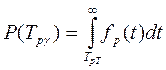

Де fp(t) - густина розподілення ресурсу.

Наприклад у випадку розподілення Вейбула

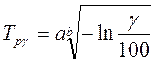
У випадку експонційного розподілення:

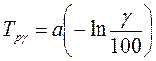
Де 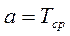- середнє напрацювання на відмову.

До кількісних показників довговічності відносяться також середній ресурс, медіанний ресурс і середній термін служби.

Середній ресурс:

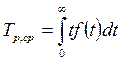або

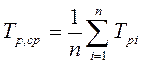
де Трі - ресурс і -го компонента.

Медіанний ресурс Тр,м- визначають із виразу:

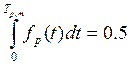0

Середній термін служби:

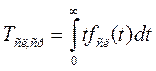
Де fсл(t)- густина розподілення терміну служби.

В кінцевій сукупності (партії) виробництва

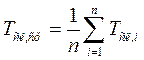
де Тсл, і - термін служби і-го виробу.

Гама-процентний і медіанний термін служби можна визначити аналогічно визначенню Тр, м; Гр,у.

Кількісний показник ремонтоздатності - імовірність відновлення за даний період часу

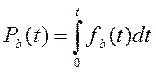
Де fB(t) - густина розподілення часу відновлення