Нахождение истинных и средних теплоемкостей

Для нахождения истинной массовой, объемной или молярной теп­лоемкости используют два способа: графический – по c,t–диаграмме и табличный – с использованием специальных таблиц.

В c,t–диаграмме по оси ординат откладываются значения истинной теплоемкости (массовой, объемной или молярной), а по оси абсцисс – температуры.

Пусть истинная удельная теплоемкость на c,t–диаграмме изображается линией 1-2, которая в общем случае являет­ся кривой (рис 3.4.1).

Рис. 3.4.1. Графическое определение средней теплоемкости

в заданном интервале температур

Тогда отрезок 4-1 в масштабе будет истинной удельной теплоемкостью при температуре t_l, a отрезок 3-2 – истинной удель­ной теплоемкостью при темпе­ратуре t₂.

Если заменить площадь 1234 равновеликим ей прямоуголь­ником l'2'З4 с основанием 4–3, то высота его 4–1' (или 3-2') и бу­дет представлять в масштабе среднюю удельную теплоем­кость с в процессе 1-2.

Площадь этого прямоуголь­ника равна произведению высо­ты на основание или в данном случае произведению: А = с_m(t₂– t₁).

Умножим пра­вую и левую части уравнения для средней массовой теплоемкости на разность температур (Т₂–Т₁), по­лучим: q_1,2=c_m(Т₂–Т₁)

Сопоставляя правые части последних уравнений, видим, что они равны, поэтому пл. 1234, равнове­ликая пл. 1'2'34, определяет в масштабе удельную подве­денную (или отведенную) теплоту.

Следовательно, на c,t–диаграмме площадь, ограниченная линией истинной удельной теплоемкости, крайними орди­натами этой линии и осью абсцисс, определяет в масштабе удельное количество подведенной или отведенной теплоты.

Задача определения средней удельной теплоемкости в заданном процессе значительно упрощается, если линию истинной теплоемкости представить в виде прямой (рис. ).

В этом случае средняя удельная теплоемкость в интер­вале температур t₁–t₂ может быть принята как среднеарифметическая между истинными теплоемкостями с₁ (при темпе­ратуре t₁) и с₂ (при температуре t₂) (рис.3.4.2, а), т. е.

.

Задача нахождения средней удельной теплоемкости (в случае прямолинейной зависимости теплоемкости от темпе­ратуры) может быть еще упрощена, если в качестве ее взять истинную удельную теплоемкость при среднеарифметиче­ской температуре процесса, т.е. при температуре 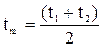(рис. 3.4.2, б).

Рис. 3.4.2. Определение средней теплоемкости в заданном интервале температур упрощенным способом

Замена криволинейной зависимости теплоемкости от тем­пературы прямолинейной зависимостью вносит некоторую неточность в расчеты, однако незначительную, и поэтому часто ею можно пренебречь.

Нахождение теплоемкостей табличным способом произ­водится с помощью таблиц молярных или удельных теплоемкостей.

В таблице 3 приложения приведены истинные массовые теплоем­кости, часто встречающиеся в тепловых расчетах воздуха и отдельных газов.