Смеси идеальных газов

Каждый отдельный газ, входящий в смесь, называют компонентом газовой смеси. Любой компонент ведет себя как бы независимо от других газов, т. е. занимает полный объем смеси и оказывает на стенки сосуда свое давление, называемое парциальным давлением.

Закон Дальтона справедлив только для идеальных газов и формулируется так: давление смеси газов равно сумме парциальных давлений газов, составляющих смесь: ,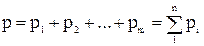

где р₁, р₂, …, р_m – парциальные давления газов.

Следовательно, парциальным давлением газа называется такое давление, которое имел бы данный газ, входящий в смесь, если бы он один занимал весь объем смеси газов при температуре смеси.

При расчете газовой смеси обычно определяют молярную массу, удельную газовую постоянную, плотность, теплоемкости, парциальное давление и объем компонентов, образующих смесь. Для того чтобы это сделать нужно знать, из какого количества и каких газов состоит газовая смесь, т. е. необходимо задать эту смесь по составу. Состав смеси газов может быть задан массовыми или объемными долями.

Массовой долей называют отношение массы данного газа (компонента), входящего в смесь, к массе смеси газов. Обозначается массовая доля буквой g:

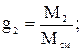
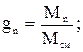
где g₁ g₂ … g_n – массовые доли отдельных газов в смеси; М₁, М₂, М_n – массы этих газов; М_см –масса смеси; n – число компонентов в смеси.

Из приведенных соотношений очевидно: ,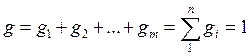

т. е. сумма всех массовых долей равна единице.

Объемной долей называют отношение парциального (приведенного) объема газа, входящего в смесь, к объему смеси. Парциальным объемом газа называют объем, который занимал бы данный газ, если бы его температура и давление равнялись температуре и давлению смеси газов. Сумма парциальных объемов равна объему смеси газов. Обозначается объемная доля буквой r.

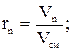
где r₁, r₂, r_n – объемные, V₁, V₂, V_n – парциальные объемы газов, входящих в смесь; V_см – объем смеси газов. Тогда из соотношений следует: 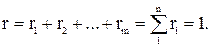Сумма всех объемных долей равна единице.

Соотношение для i –того компонента газовой смеси можно задать следующим образом: 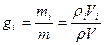, поскольку плотность i-го компонента и смеси газов берутся при одинаковых P и T, отношения этих плотностей на основании следствия из закона Авогадро. Можно заменить отношением молекулярных масс или же обратным отношением газовых постоянных. Тогда .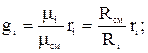

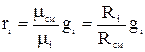Определим кажущуюся молекулярную массу смеси газов:

;

Из з-на Авогадро следует, что при одинаковых давлениях и температурах плотности прямо пропорциональны молекулярным массам: Т.е. газовая постоянная смеси газов равна сумме произведений массовой доли каждого газа на его газовую постоянную, т.к. 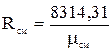. Из выше приведенных соотношений: .

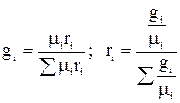Смешение газов при Т=const характеризуется равенством P_см∙V_i=P_i∙V_см или P_i=P_см∙r_i. Т.о. парциальное давление газа входящего в смесь, равно произведению давления смеси на объемную долю данного газа или через массовые доли , т.е. парциальное давление газа, входящего в смесь, равно произведению давления смеси на отношение молекулярных масс смеси и данного газа и на массовую долю газа.

Вид расчетных формул для теплоемкости смеси идеальных газов зависит от способа задания состава газовой смеси.

Если состав смеси задан массовыми долями компонентов, то массовая теплоемкость смеси, определяется как сумма произведений массовых долей на массовую теплоемкость газов, входящих в смесь:

.

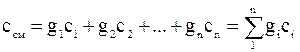Если смесь задана объемными долями компонентов, то объемная теплоемкость смеси газов будет равна сумме произведений объемных долей на объемную теплоемкость каждого из компонентов смеси:

.