Билет 13

1) В изолированной системе возможны только такие процессы, при которых энтропия системы возрастает. Т.е. dS≥ 0 или dS≥ dQ/T .

Второе начало термодинамики определяет направление термодинамических процессов и указывает на физический смысл энтропии: энтропия - мера рассеяния энергии, т.е. характеризует ту часть энергии, которую нельзя превратить в работу.

Принцип Tомсона - процесс, при котором работа переходит в тепло без количественных изменений состояния системы, необратим, т.е. невозможно полностью преобразовать в работу всё тепло, взятое от тела, не производя никаких др. изменений состояния системы.

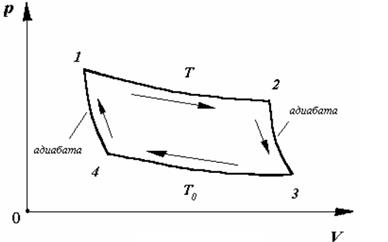
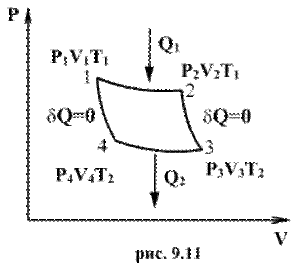
Наиболее совершенным в отношении КПД является цикл Карно, который состоит из двух изотерм (1-2, 3-4) и двух адиабат (2-3, 4-1).

При изотермическом расширении от нагревателя отбирается тепло Q₁ (на участке 1-2). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны P₂V₂T₁. На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до T₂. Параметры точки 3 – P₃V₃T₂ . На участке 3-4 газ изотермически сжимается. Параметры точки 4 - P₄V₄T₂. Выделяющееся при этом тепло Q₂ отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл “1-2-3-4-1 и в итоге нагреватель отдал газу теплоту Q₁ , а холодильник отобрал Q_{2 .} Разность Q₁ - Q₂ определяет полезную работу газа за один цикл, так как согласно I началу термодинамики бQ =бA + dU , но для кругового процесса dU=0 и, следовательно бQ=бA.

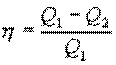Определим коэффициент полезного действия цикла Карно для обратимого процесса. Теплота подводится на участке 1-2 и отводится на участке 3-4. Для изотермического процесса внутренняя энергия Q=const и все подводимое тепло расходуется на работу Q_1.= A.

Тогда

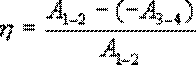или

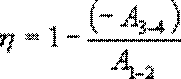
Для изотермического процесса работа

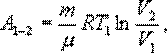
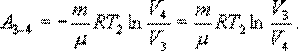
С учетом последних выражений

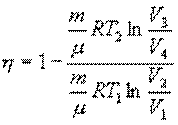Покажем, что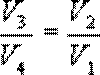

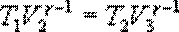Так как процессы на участках 2-3 и 1-4 адиабатические, для определения связи между V₃ и V₂ и V₂ и V₄ используем уравнение Пуассона в виде Следовательно, и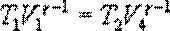

Разделим эти уравнения и получим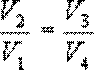

Тогда выражение для к.п.д. (9.24) примет вид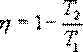

Эта формула справедлива только для обратимого цикла Карно.

2.

Энтропия системы физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно полученному или отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс. Энтропия, подобно внутренней энергии, является однозначной функцией состояния системы.

Бесконечно малое изменение энтропии определяется соотноше-

нием dS=dQ/T

При переходе системы из одного состояния в другое, изменение эн-

тропии можно рассчитать так

S=S2-S1=12dQ/dT

На основании первого начала термодинамики

dQ=dU+dA=CvdT+pdV=CvdT+RT/V*dV

тогда

dQ/T=Cv*dT/T+R*dV/V

S=S2-S1=T1T2V1V2dQ/dT=Cv*lnT2/T1+R*lnV2/V1

Известно, что при изотермическом процессе T = const, т.е. T1=T2,

тогда S= R*lnV2/V1

Пр изохориическом процессе V = const, т.е. V2 = V1. Таким образом

S=Cv*lnT2/T1