ЛЕКЦІЯ 5

Канонічна модель плану станції (частина 1)

Канонічна модель плану колійного розвитку станції повинна забезпечити:

– вхідний контроль введеної інформації;

– можливість зміни окремих параметрів схеми, заданих за умовчанням;

– аналіз, автоматичне розпізнавання типових елементів схеми колійного розвитку і вибір програмних модулів для розрахунку;

– комплексний розрахунок плану колійного розвитку і побудова вихідної моделі.

Для реалізації процедур автоматизованого синтезу колійного розвитку станцій найбільш прийнятними є ГМ, що засновані на зважених орграфах. До складу канонічної моделі станції повинні входити топологічна і параметрична моделі. Топологічна модель відображає склад елементів станції (колії, стрілочні переводи, сполучні криві та ін.), їх взаємне розташування і взаємозв'язок. Параметрична модель містить відомості про форму і геометричні розміри відповідних елементів.

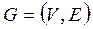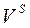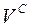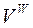Топологічна модель станції є орієнтований граф , в якому виділено три підмножини вершин: , і . Вершини 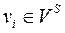є центрами стрілочних переводів (ЦП), вершини 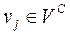– вершинами кутів повороту кривих (ВКП), вершини 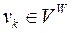– кінцями колій (КК). Дуга графа 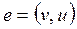позначається впорядкованою парою, що складається з початкової 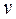і кінцевої 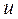вершин; її напрям задано від вершини 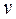до вершини 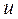. Прийнято, що всі дуги орієнтовані зліва направо.

Ступінь вершини орієнтованого графа 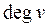визначається числом інцидентних їй дуг

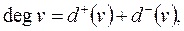
де 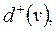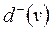– відповідно напівступені виходу і заходу вершини 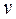, які визначаються як множина всіх дуг, що виходять з вершини 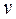і заходять в не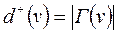ї,

і ,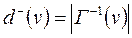

де 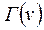– множина вершин, що є кінцевими вершинами дуг, у яких початковою вершиною є ;

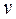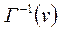– множина вершин, що є початковими вершинами дуг, у яких кінцевою вершиною є .

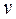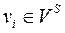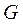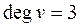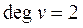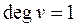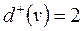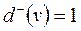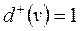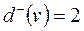Напівступені вершин орієнтованого графа дозволяють ідентифікувати тип вершини (ЦП – , BКП – , KК – ), а також визначити напрям укладання стрілочних переводів (якщо і – перевід протишерстний; якщо і – перевід пошерстний). Максимальний напівступінь кожної вершини не перевищує двох.

Згідно з теорією графів сума напівступенів виходу всіх вершин графа дорівнює сумі напівступенів заходу і дорівнює числу його дуг

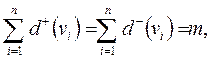
де 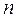, 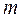– відповідно число вершин і дуг графа .

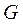Дане твердження використовується для вхідного контролю даних про схему станції.

Для представлення орієнтованого графа станції в ЕОМ прийнята структура даних, що називається списками інцидентності. Вказані списки містять для кожної вершини 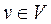список вершин 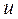таких, що 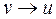. При цьому, оскільки напівступінь виходу кожної вершини графа 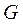не перевищує двох, то для представлення кожного списку достатньо двох змінних в пам'яті ЕОМ.

Для розділення множини вершин графа 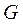на підмножини 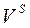, 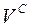і 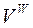кожному з них виділені непересічні групи номерів: , , .

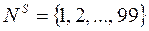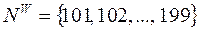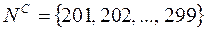Нижче наведено приклад списків інцидентності вершин 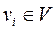графа 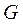, показаного на рис. 2 (табл. 3).

Перший стовпець матриці є списком всіх вершин графа; в рядках двох інших стовпців – списки інцидентності відповідних вершин.

Таблиця 3 – Списки інцидентності вершин орграфа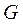

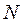
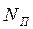
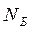
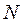
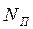
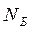
	+14			+3
	+4
		+18
	+1

Для зручності аналізу схем станцій прийнято, що першим в списку для вершин 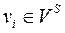з напівступенем виходу 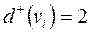(протишерстні переводи) указується номер вершини 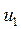, з якою дана стрілка (вершина 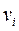) зв'язана по прямій колії (звичайний перевід) або правій колії (симетричний перевід); другим в списку указується номер іншої вершини 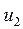, суміжної з .

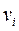Для вершин 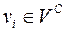з напівступенем виходу 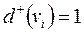(ВКП, ЦП пошерстних стрілок) другий елемент списку відсутній. Для вершин 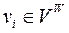з напівступенем виходу 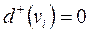(КК) відсутні обидва елементи списку.

Рисунок 2 – Орграф G=(V,E) схеми станції А

Слід зазначити, що при прийнятому способі представлення орграфа 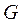для деяких вершин 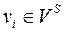, 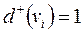(ЦП пошерстних стрілок) неможливо визначити з моделі кути нахилу суміжних відрізків. Тому за наявності вхідної моделі, ці кути встановлюються на підставі екранних координат вершин відрізків, а при табличному введенні внутрішньої моделі в списках інцидентності необхідно кінцеві вершини дуг, що заходять в такі ЦП по прямій колії, помітити знайомий «+».