Вимоги до математичних моделей, призначених для автоматизованого проектування. Класифікація математичних моделей

Математичні моделі служать для опису властивостей об'єктів у процедурах автоматизованого проектування. Якщо проектна процедура включає створення математичної моделі і оперування нею з метою отримання корисної інформації про об'єкт, то говорять, що процедура виконується на основі математичного моделювання.

До математичної моделі висуваються вимоги універсальності, точності, адекватності та економічності.

Ступінь універсальності математичної моделі характеризує повноту відображення в моделі властивостей реального об'єкта. Математична модель відображає лише деякі властивості об'єкта. Так, більшість математичних моделей, використовуваних при функціональному проектуванні, призначена для відображення фізичних або інформаційних процесів, що протікають в об'єкті, при цьому не потрібно, щоб математична модель описувала такі властивості об'єкта, як геометрична форма складових його елементів.

Точність математичної моделі оцінюється ступенем збігу значень параметрів реального об'єкта і значень тих же параметрів, розрахованих за допомогою оцінюваної математичної моделі.

Адекватність математичної моделі – здатність відображати задані властивості об'єкта з похибкою не вище заданої. Оскільки вихідні параметри є функціями векторів параметрів зовнішніх Q та внутрішніх Х, похибка 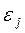залежить від значень Q і Х. Звичайно значення внутрішніх параметрів математичної моделі визначають з умови мінімізації похибки 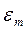в деякій точці Q_ном простору зовнішніх змінних, а використовують модель з розрахованим вектором Х при різних значеннях Q. При цьому, як правило, адекватність моделі має місце лише в обмеженій області зміни зовнішніх змінних – області адекватності (ОА) математичної моделі

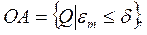
де 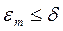– задана константа, рівна гранично допустимій похибці моделі.

Економічність математичної моделі характеризується затратами обчислювальних ресурсів (витратами машинних часу Т_м і пам'яті П_м) на її реалізацію. Чим менше Т_м і П_м, тим модель економічніша. Замість значень Т_м і П_м, залежних не тільки від властивостей моделі, але і від особливостей застосовуваної ЕОМ, часто використовують інші величини, наприклад: середня кількість операцій, які виконуються при одному зверненні до моделі, розмірність системи рівнянь, кількість використовуваних в моделі внутрішніх параметрів і т.п.

Вимоги високої точності, ступеня універсальності, широкої ОА, з одного боку, і високої економічності, з іншого боку, суперечливі. Найкраще компромісне задоволення цих суперечливих вимог залежить від особливостей вирішуваних завдань, ієрархічного рівня і аспекту проектування. Ця обставина обумовлює застосування в САПР широкого спектру математичних моделей.

Математичні моделі класифікуються за наступними ознаками:

– характером відображуваних властивостей об'єкта;

– приналежністю до ієрархічного рівня;

– ступенем деталізації опису всередині одного рівня;

– способом представлення якостей об’єкта;

– способом отримання моделі.

За характером відображуваних властивостей об'єкта математичні моделі бувають структурні і функціональні, за приналежністю до ієрархічного рівня – математичні моделі мікрорівня, макрорівня і метарівня, за ступенем деталізації опису всередині одного рівня – повні і макромоделі, за способом представлення якостей об’єкта – аналітичні, алгоритмічні та імітаційні, за способом отримання моделі – теоретичні і емпіричні.

Структурні математичні моделі призначені для відображення структурних властивостей об'єкта. Розрізняють структурні математичні моделі топологічні та геометричні. У топологічних математичних моделях відображаються склад і взаємозв'язок елементів об'єкта. Їх найчастіше застосовують для опису об'єктів, що складаються з великого числа елементів, при вирішенні завдань прив'язки конструктивних елементів до певних просторових позицій (наприклад, завдання компонування устаткування, розміщення деталей, трасування з'єднань) або до відносним моментам часу (наприклад, при розробці розкладів, технологічних процесів).

Топологічні моделі можуть мати форму графів, таблиць (матриць), списків і т.п.

У геометричних математичних моделях відображаються геометричні властивості об'єктів. В них додатково до відомостей про взаємне розташування елементів містяться відомості про форму деталей. Геометричні математичні моделі можуть виражатись сукупністю рівнянь ліній і поверхонь, алгебраїчних співвідношень, що описують області, які складають тіло об'єкта; графами і списками, що відображають конструкції з типових конструктивних елементів, і т.п.

Геометричні математичні моделі застосовують при вирішенні завдань конструювання. Використовують кілька типів геометричних математичних моделей. Для відображення геометричних властивостей з порівняно нескладними поверхнями застосовують математичні моделі, що подаються в аналітичній або алгебраїчній формі (аналітичні, алгебрологічні).

Аналітичні математичні моделі – рівняння поверхонь і ліній. В алгебрологічних математичних моделях тіла описуються системами логічних виразів, що відображають умови приналежності точок внутрішнім областям тіл.

Для складних поверхонь аналітичні та алгебрологічні моделі виявляються занадто громіздкими. Їх важко отримувати і незручно використовувати. Область їх застосування зазвичай обмежується поверхнями плоскими і другого порядку.

Для відображення геометричних властивостей деталей зі складними поверхнями застосовують математичні моделі каркасні і кінематичні.

Каркасні математичні моделі представляють собою каркаси – кінцеві безлічі елементів, наприклад, точок або кривих, що належать поверхні, що моделюється. Зокрема, вибір каркаса у вигляді ліній, що утворюють сітку на поверхні, що описується, призводить до розбиття поверхні на окремі ділянки. Кусково-лінійна апроксимація на цій сітці усуває головний недолік аналітичних моделей, оскільки в межах кожної з ділянок, що мають малі розміри, можлива задовільна за точністю апроксимація поверхнями з простими рівняннями. Коефіцієнти цих рівнянь розраховуються виходячи з умов плавності сполучень ділянок.

У кінематичних математичних моделях поверхня представляється в параметричному вигляді. Таку поверхню можна отримати в результат переміщення в тривимірному просторі кривої, що називається утворюючою, за деякою направляючою лінією.

Коефіцієнти рівнянь у всіх розглянутих моделях, як правило, не мають простого геометричного сенсу, що ускладнює роботу з ними в інтерактивному режимі. Цей недолік усувається в канонічних моделях і в геометричних макромоделях.

Канонічні моделі використовують у тих випадках, коли вдається виділити параметри, що однозначно визначають геометричний об'єкт і в той же час мають простий зв'язок з його формою.

Геометричні макромоделі є описами попередньо відібраних типових геометричних фрагментів. Такими фрагментами можуть бути типові складальні одиниці, а їх макромоделі – умовні номери, габаритні і стикувальні розміри. При оформленні конструкторської документації макромоделі використовують для опису типових графічних зображень.

Функціональні математичні моделі призначені для відображення фізичних або інформаційних процесів, що протікають в об'єкті при його функціонуванні або виготовленні. Зазвичай функціональні математичні моделі являють собою системи рівнянь, що зв'язують фазові змінні, внутрішні, зовнішні та вихідні параметри.

Одним з основних завдань створення САПР є розробка компонентів математичного забезпечення, що забезпечують найкраще компромісне задоволення суперечливих вимог універсальності, точності, економічності, надійності.

Використання принципів блочно-ієрархічного підходу до проектування призводить до появи ієрархії математичних моделей об’єктів, що проектуються.

Кількість ієрархічних рівнів при моделюванні визначається складністю об'єктів, що проектуються, і можливостями засобів проектування.

Однак для більшості предметних областей можна віднести наявні ієрархічні рівні до одного з трьох узагальнених рівнів: мікро-, макро- і метарівня.