Основні відомості про сіті Петрі

Особливістю сітей Петрі є їх придатність бути інструментом графічного зображення системи у вигляді блок-схеми, у якій діють паралельні процеси, тобто паралельна обробка інформації , а також безпосередньо паралельно діючі об’єкти.

Сіті Петрі визначаються як модифікований, багатофункціональний, зважений дводольний граф. Останнє означає, що всі вершини графа відносяться до двох типів: позиції (місця) 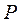та переходи 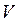. Позиції зображуються кільцем, а переходи – відрізками прямих. Дуги у сітях Петрі – напрямні. Причому, кожна дуга зв’язує вершини тільки різних типів. Дуги позначаються відповідними значеннями ваги (цілими числами), і дугу з вагою 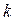можна вважати еквівалентною 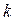паралельним дугам. У задачах моделювання, де використовуються поняття умов (станів) і подій, позиції (місця) відповідають умовам, а переходи – подіям. Кожний перехід (подія) пов’язаний з певним числом вхідних і вихідних позицій – аналогів відповідно передумов та післяумов цієї події. На малюнку 3.6 наведені приклади зображення дводольних графів.

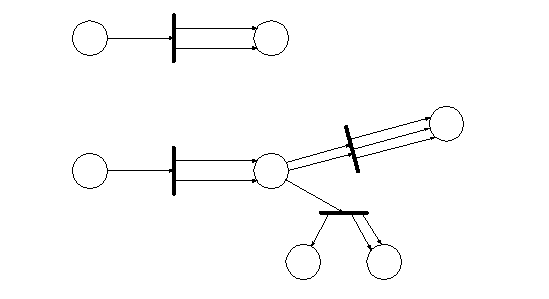
Мал. 3.6

Оригінальним поняттям сітей Петрі є поняття «фішки». Фішки зображуються точками, розташованими всередині позицій. Таким чином, кожній позиції сіті ставиться у відповідність натуральне число, яке вказує кількість фішок у даній позиції – розмітку позиції. Сукупність таких чисел для всіх позицій сіті називають розміткою сіті. Якщо позиція не містить фішок, то вона має нульову розмітку. Приклад сіті з розміткою наведений на малюнку 3.7.

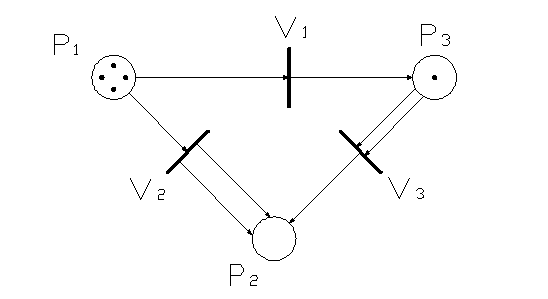
Мал. 3.7

Важливим поняттям сітей Петрі є поняття «спрацьовування переходів», яке полягає у вилученні фішок з кожної вхідної позиції та переміщення їх у кожну вихідну позицію. Причому, кількість фішок, які вилучаються з конкретної позиції або переміщуються у конкретну позицію, дорівнює кількості дуг, що з’єднують перехід, що спрацьовує, із даною конкретною позицією. Так, наприклад, перехід 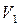на мал. 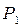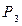3.7 при спрацьовуванні вилучає з позиції одну фішку та збільшує кількість фішок у позиції на одну. Перехід 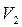вилучає одну фішку з позиції 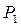та переміщує у позицію 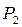дві фішки.

Сітка Петрі функціонує, переходячи від розмітки до розмітки, наприклад, від деякої початкової до деякої проміжної або до заключної – тупикової розмітки, тобто такої, коли не може спрацьовувати жодний перехід. Це означає, що спрацьовування переходів змінює розмітку сіті. Власно кажучи, предметом теоретичного дослідження сітей Петрі є процес їх функціонування, тобто аналіз можливих послідовностей спрацьовування переходів, і властивості розміток сіті, які при цьому отримують.

Інтерпретація спрацьовування переходів може бути сформульована так. Перехід може спрацювати тоді і тільки тоді, коли всі його вхідні місця заповнені хоча б однією фішкою. Перехід при спрацьовуванні вилучає рівно по одній фішці з кожного свого вхідного місця і утворює рівно по одній новій фішці в кожному своєму вихідному місці. Якщо в сітці Петрі є один перехід, який може спрацьовувати, він обов’язково це зробить. Якщо можуть спрацьовувати два або більше переходів, то вони спрацьовуватимуть послідовно, але не детерміновано, тобто не можна заздалегідь знати, який перехід повинен спрацьовувати. Наприклад, на мал. 3.7 перехід 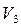не може спрацьовувати, оскільки у позиції 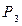міститься тільки одна фішка, а дуг, що пов’язують 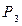і 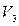- дві. Але, якщо спрацьовував перехід 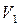, то внаслідок збільшення кількості фішок у позиції 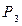перехід 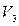спрацьовуватиме. Тобто, саме введення поняття «спрацьовування переходів» дає підставу для моделювання процесів, які пов’язані між собою причинно-наслідковим зв’язком.

Сітям Петрі притаманні певні властивості. Деякі з них:

Безпека. Місце сіті Петрі, яке містить не більше однієї фішки, називається безпечним. Сітка Петрі безпечна, коли безпечні всі місця сіті.

Обмеженість. Властивість не допускати перевищення кількості фішок у конкретній або довільній позиції деякого довільного числа. Місце є 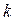- безпечним або 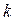- обмеженим, якщо кількість фішок у ньому не перебільшує цілого числа .

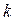Одна з основних проблем у теорії сітей Петрі – задача про скінченність функціонування сіті, тобто про досяжність тупикової розмітки.

Формально сітку Петрі 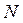визначають п’ятіркою значень

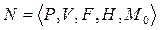, (3.6)

де 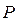- скінченна, непуста множина місць або позицій 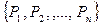; 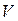- скінченна непуста множина переходів 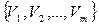; 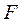- функція інцидентності, яка вказує на наявність дуг, що з’єднують місця з переходами; 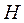- функція інцидентності, яка вказує на наявність дуг, що з’єднують переходи з місцями; 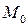- початкова розмітка сіті.

Функції інцидентності 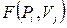( 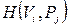) складаються з множини двох значень 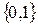: 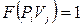, коли з вершини-місця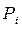 прямує дуга до вершини-переходу 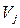( 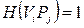, коли з вершини-переходу 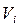прямує дуга до вершини-місця 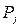), у протилежних випадках, тобто, коли відповідних дуг не існує, ( ).

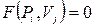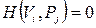Розглянемо довільну сітку Петрі (мал. 3.8), яка у відповідністю з формою завдання (3.1), може бути описаною так:

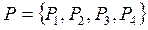- множина позицій (місць);

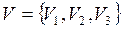- множина переходів;

початкова розмітка :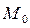

=

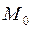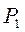
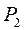
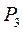
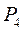
функції інцидентності:

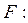
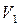
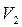
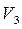
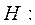
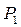
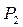
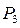
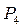
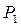
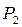
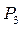
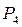
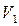
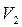
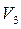
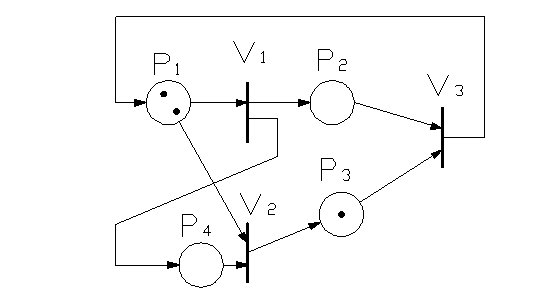
Мал. 3.8

Результати функціонування сіті Петрі зведені у таблицю, де наведені декілька можливих змін розміток сіті, починаючи з .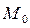

Розмітка	Позиції (місця)

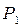
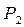
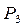
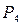
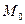
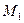
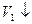
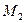
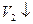
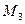
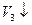
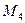
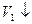
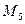
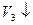
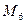
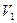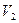
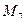
Пояснення до таблиці. При початковій розмітці (перший рядок) лише один перехід 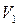може спрацьовувати. Відбувається зміна розміток (другий рядок). При розмітці 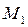до спрацьовування готові всі три переходи 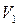, , 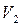, 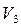але може спрацьовувати лише один, нехай ”випадково” спрацює перехід 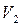, тоді утворилась розмітка 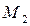, при якій може спрацьовувати тільки перехід 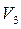, і т. і. Останній крок при розмітці 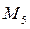у випадках спрацьовування одного з двох можливих переходів призводить до тупикових розміток: відповідн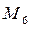о або .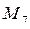

Можна повернутися до розмітки 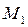, коли до спрацьовування готові всі три переходи і самостійно розглянути кроки функціонування сіті Петрі у випадках, коли можуть спрацьовувати переходи 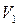або 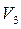, і побудувати аналогічні таблиці розміток.

Дерево досяжності – це множина досяжності розміток сіті Петрі. Початковою вершиною дерева є вершина, яка відповідає початковій розмітці 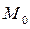. Кожна можлива послідовність розміток до своєї тупикової утворює одну гілку дерева досяжності (наприклад, послідовність у наведеній таблиці) з вершинами, які відповідають розміткам на кожному кроці і поєднані стрілками. Дерево ”розростається” при розгляданні спрацьовування всіх можливих переходів на кожному кроці.