Сіткові моделі задач про максимальний потік

Ці задачі відносяться до дуже розповсюджених задач, в яких відбиваються транспортні моделі і використовується теорія графів.

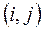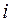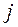По сітці магістралей(транспортних, трубопроводів), тобто по ребрах , де , - номери вершин, які поєднуються відповідними ребрами ( 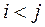), направляється ресурс (речовина, вантаж, інформація) від входу (витоку) 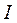графа до його виходу (стоку) 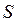. Максимальна кількість речовини 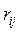, яку може пропустити за одиницю часу ребро 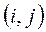, називається його пропускною спроможністю. В загальному випадку 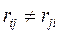. Якщо вершини 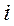та 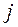на сітці не з’єднані, то 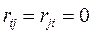. Пропускні спроможності ребер вздовж прямого та зворотного напряму зазвичай показують у дужках на графі, а також їх можна задати квадратною матрицею, розмір якої визначається кількістю вершин на сітці.

Кількість 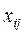речовини, що проходить через ребро 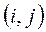за одиницю часу, називається потоком по ребру. В теорії потоків припускається, що, якщо від вершини 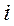до вершини 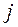направляється потік величиною 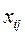, величина потоку в зворотному напрямі дорівнює 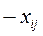, тобто

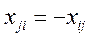. (3.2)

Приймається також, .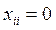

Сукупність 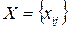потоків вздовж усіх ребер 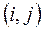сітки називають потоком на сітці, або просто потоком.

Потік вздовж кожного ребра не перебільшує його пропускну здатність

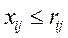
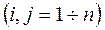, (3.3)

де 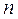- кількість вершин сітки.

Кількість речовини, що втікає у вершину, дорівнює кількості речовини, що витікає з неї

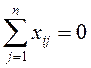
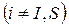. (3.4)

Властивості (3.2) 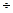(3.4), які вважаються основними обмеженнями потоків по ребрах, необхідно враховувати при формуванні потоку на сітці.

Алгоритм знаходження максимального потоку вимагає введення поняття розрізу сітки, що визначає множину ребер, при вилученні яких повністю припиняється потік від витоку до стоку, тобто фактично розріз складається з двох підмножин ребер, які не перетинаються: в одній підмножині 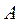міститься витік 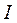, у другій 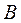– стік 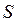. Пропускна спроможність розрізу дорівнює сумі пропускних спроможностей „розрізаних” ребер і позначається 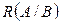, тобто

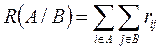. (3.5)

Якщо на сітці заданий деякий потік 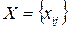, то ребро 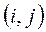називають насиченим, якщо величина потоку по цьому ребру збігається з його пропускною здатністю, і ненасиченим, якщо потік менше його пропускної здатності.

Величина

,

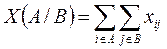яка складає суму потоків 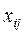по всіх ребрах розрізу, називається потоком через розріз.

У теорії задач на максимальний потік на сітці важливе значення має теорема Форда-Фалкерсона: на будь якій сітці максимальна величина потоку від витоку 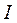до стоку 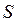дорівнює мінімальній пропускній спроможності розрізу, що відділяє 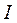від .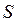

Наведемо алгоритм побудування максимального потоку, для розуміння теоретичної обґрунтованості якого варто додатково ознайомитись з описанням більш детального алгоритму, пов’язаного зі складанням матриць пропускних спроможностей 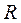, потоків 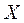та матриці їх різниць 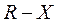, наприклад, в МВ №3534. Отже,

1. Будуємо деякий початковий потік 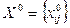. В якості рекомендації можна взяти до уваги, що цей потік доцільно починати від витоку 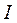по ребру з більшою пропускною спроможністю. Потік ілюструється ланцюгом відповідних вершин, що поєднуються відрізками прямих, а саме ребер, над якими показують перенесені з сітки пропускні спроможності .

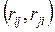2. Фіксуємо мінімальну пропускну спроможність ланцюга першому значенню потоку 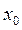, який стане першим доданком сумарного потоку і одночасно значенням 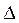, на яке корегується пропускні спроможності ланцюга, тобто .

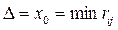3. Створюємо скорегований ланцюг пропускних спроможностей у виписаному ланцюзі під відрізками, що позначають ребра, віднімаючи 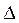від пропускної спроможності у напрямі руху потоку і додаючи значення 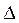до пропускної спроможності у протилежному русі: .

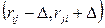4. Якщо хоча б одне зі значень 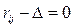, то ребро стає насиченим, помічаємо його хрестиком і обираємо наступний потік в обхід насиченого ребра. Якщо жодна різниця не дорівнює нулю, наступний потік може завершити доведення одного з ребер початкового потоку до насиченого.

5. Процес створення потоків 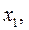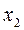,…, 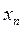в рамках наведених пунктів алгоритму продовжується до тих пір, доки на шляху до стоку 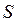сформується хоча б один розріз, який проходить по насичених ребрах, тобто використані всі можливі шляхи формування нових потоків.

6. Знаходиться отриманий сумарний потік 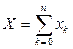, який і повинен бути максимальним, що треба підтвердити перевіркою теореми Форда-Фалкерсона.

4.4. Задачі сітьового планування та управління на залізничних станціях

Важливим напрямком використання теорії графів є розповсюдження її на задачі планування та управління виробничими процесами, зокрема, на залізничному транспорті. Особливості методів сітьового планування та управління (СПУ) полягають у можливості в графічній формі відбити виробничий процес, показати послідовність та логічний взаємозв’язок окремих робіт, які створюють процес, виявити критичні, тобто ті, що визначають його хід, роботи та зосередити на них увагу.

СПУ ґрунтується на побудуванні орієнтовного графа станів виробничого процесу, в якому вершини – це події, які відбивають умови можливості початку або закінчення різноманітних робіт, а ребра – операції, які складають саме виробничий процес, тобто безпосередньо роботи.

Події нумерують послідовно. Кожну роботу позначають номерами подій, що її обмежують. Ребра графа є зваженими тривалістю роботи у певному масштабі часу. Будь-яка послідовність робіт визначає шлях. СПУ має на меті такі задачі:

1. Науковий аналіз і розробка технологічних процесів. Це означає оптимізацію сітьового графіка, тобто находження такого порядку всіх робіт та розподілу між ними ресурсів таким чином, щоб забезпечити виконання всього процесу за мінімальний термін (оптимізація за часом) та з мінімальними витратами (оптимізація за вартістю). Це досягається порівнянням варіантів сітьового графіка та його послідовного поліпшення.

2. Оперативний контроль за ходом процесу. Методи СПУ дозволяють на кожному етапі виділяти головні (критичні) роботи, на які треба звернути особливу увагу. До розряду критичних на кожному етапі можуть потрапляти різні роботи в залежності від обстановки та фактичного ходу процесу.

Основу сітьового графіка складають три елементи: робота, подія, шлях.

Робота – це самостійна трудова операція. Серед робіт розрізняють такі типи:

- дійсна – трудовий процес, який вимагає часу і ресурсів (наприклад, технічний огляд составу, подача вагонів під навантаження ін.);

- очікування – технологічна операція, яка потребує часу без витрат ресурсів (наприклад, технологічна перерва у маневровій роботі через пропускання пасажирського потягу, операція зупинки якогось приладу при підготовці його до ремонту та ін.);

- фіктивна – указує тільки на логічний зв’язок між роботами і не потребує ані часу, ані ресурсів.

Дійсну роботу та очікування відмічають на графіку суцільними стрілками, а фіктивну – штриховими.

Подія – фіксований факт, який визначає закінчення або можливість початку декількох робіт, момент, який фіксує певний стан виробничого процесу (не має тривалості). Її треба сформулювати в категоричній формі. Наприклад: «Технічний огляд потягу завершений». Це означає готовність до виконання наступної роботи. У кожної роботи є початкова та кінцева подія. Роботу не можна почати, доки не здійсниться її початкова подія. Подія же не може статися, доки не будуть виконані всі роботи, для яких вона вважається кінцевою. Розрізняють проміжні, первинні (початкові) та завершальні події.

Шлях – будь-яка послідовність робіт, яка поєднує деякі дві події. Тривалість його дорівнює сумарній тривалості робіт, які складають його. Розрізняють такі шляхи:

- повний – послідовність робіт, які поєднують первинну та завершальну події;

- передуючий події;

- наступний за подією;

- проміжний між подіями;

- критичний – найбільший повний шлях.

На сітьовому графіку завжди декілька повних шляхів. Максимальний з них є критичним. Його тривалість визначає загальний термін виконання процесу. Формулюється задача оптимізації сітьового графіка за критерієм мінімізації цього терміну. Для цього необхідно вишукати способи скорочення критичного шляху, контролювати виконання робіт, які утворюють критичний шлях, та вживати оперативних заходів для попередження їх зриву. Саме наочність зображення послідовності робіт, якою визначається загальний термін виконання процесу, і є важливою перевагою сітьового графіка перед іншими методами планування і контролю.

Існують певні правила побудови сітьових графіків.

1. У кожної роботи номер початкової події повинен бути меншим за номер кінцевої. Послідовність подій встановлюють за рангом, тобто після викреслювання робіт, які виходять з попередньо пронумерованих подій (починаючи з початкової, до якої не входить жодної роботи), до одного рангу відносять ті, до яких не входить жодної роботи, і нумерують їх у довільному порядку і так далі.

2. Кожна проміжна подія повинна мати хоча б одну передуючу та наступну роботу (за виключенням постачання матеріалів, обладнання тощо, які зображують як роботи, що прямують з події, до якої не входить жодна робота).

3. Жоден шлях не повинен проходити двічі крізь одну і ту ж подію, тобто на сітці не повинен утворюватись замкнений цикл.

4. Між подіями може знаходитись тільки одна робота. Для зображення паралельних робіт до сітки вводять фіктивні роботи та додаткові події (малюнок 3.1).

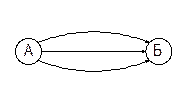
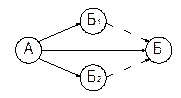
невірно	вірно

Мал. 3.1

5. Правило зображення складених робіт, тобто таких, які можуть бути розпочаті тільки після виконання деякого комплексу робіт, полягає у тому, що ці роботи зображують як сукупність послідовних робіт, результати яких є необхідними і достатніми для початку наступних робіт: якщо роботу БД можна розгорнути тільки після виконання роботи АБ, а БВ і БГ – до її закінчення, то роботу АБ треба розбити додатковими подіями на такі частки, виконання яких забезпечить можливість початку робіт БВ і БГ (малюнок 3.2).

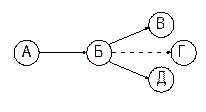невірно

вірно

Мал. 3.2

6. Правило зображення диференціально-залежних робіт, тобто таких, для виконання однієї або декількох з групи необхідно отримати результати всіх робіт, що входять до її початкової події, а для іншої (або інших) – тільки декількох з них, то в сітку вводять додаткові події та фіктивні роботи: якщо для виконання роботи ВГ необхідні результати робіт АВ і БВ, а для БД – тільки результати БВ, тов сітку вводять додаткову подію В₁ та фіктивну роботу В₁В (малюнок 3.3).

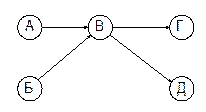невірно

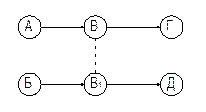вірно

Мал. 3.3

Серед параметрів, якими характеризується сітьовий графік можна відзначити такі:

- тривалість критичного шляху ;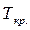

- найбільш ранній термін здійснення події 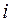- мінімально необхідний час між настанням початкової події та події 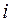, тобто максимальний шлях, який передує події 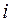: 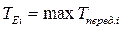. Зазвичай для початкової події ;

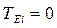- найбільш пізній припустимий термін здійснення події 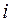- максимально припустимий час між початковою подією та подією при незмінному критичному шляху: 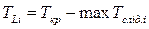, де 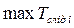- максимальний шлях, який проходить за подією. Якщо подія 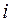розташована на критичному шляху, то 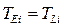. Для завершальної події ;

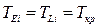- резерв часу для шляху – це різниця між тривалістю критичного шляху та тривалістю 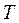шляхів, що розглядаються: 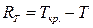. Цей параметр символізує час, на який можна збільшити тривалість усіх робіт без зміни загального терміну реалізації процесу, тобто гранично припустиме збільшення тривалості шляху 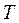, при подальшому збільшенні якої шлях стає критичним;

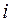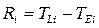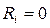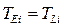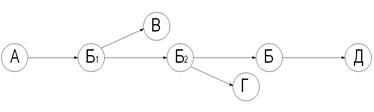
- резерв часу для події - це показник часу, на який можна затримати здійснення події, не змінюючи загального терміну виконання процесу: . Для подій, що містяться на критичному шляху, , тому що . Аналіз резервів часу для виконання кожної роботи допомагає ефективно розподілити ресурси часу між роботами. Розрізняють такі види резервів часу для роботи 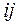(малюнок 3.4):

- повний – резерв часу максимального зі шляхів, що проходять через роботу, 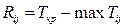. Він відбиває припустиме збільшення тривалості роботи (або спізнювання його початку), при якому довжина максимального зі шляхів, що проходять крізь неї, не перебільшить тривалості критичного шляху. При використанні цього резерву максимальний шлях через роботу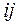 стає критичним, і всі розташовані на ньому роботи втрачають резерви часу. Величину 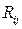зручно визначати через ранній та пізній терміни здійснення подій: ;

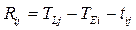- вільний (окремий) – максимальний час, на який можна збільшити тривалість роботи 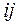(або відкласти її початок), якщо її початкова та кінцева події настануть у свої ранні терміни: 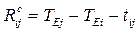. При використанні вільного резерву часу для однієї роботи не порушуються вільні резерви часу інших робіт, якщо всі події настають у свої ранні терміни;

- незалежний - утворюється лише у деяких роботах і відображає максимальний час, на який можна збільшити тривалість роботи 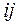(або відкласти її початок) незалежно від термінів настання її початкової та кінцевої подій: 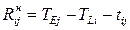. Використання незалежного резерву в будь-якому випадку не порушує резервів часу інших робіт.

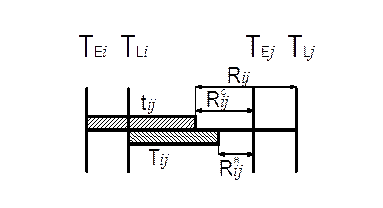
Мал. 3.4

Роботи, що розташовані на критичному шляху, не мають жодних резервів часу. Таким чином, знаючи ранні та пізні терміни здійснення подій та тривалість робіт, можна визначити параметри сітьового графіка.

Для обчислення параметрів сітьового графіка застосовують табличний, матричний та інші способи. Для порівняно невеликих графіків, які використовують при експлуатуванні залізниць, зручно обчислювати параметри саме на графіках. Для цього кожну подію – кружечок – поділяють на чотири сектори (мал. 3.5).

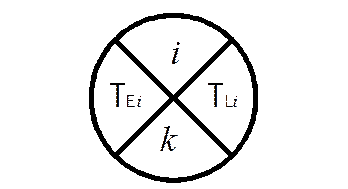
Мал. 3.5

У верхньому проставляють номер події і, інші заповнюють протягом обчислення. У лівому секторі записують ранній термін здійснення події Т_Еі, у правому – пізній Т_Lj, номер попередньої події на максимальному передуючому шляху. Починають облік з початкової події, відмічаючи Т_Еі=0, а потім обчислюють Т_Еj,послідовно переходячи від події з меншим номером до наступної за формулою 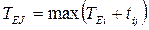, де і – номери всіх передуючих подій за кількістю вхідних до події j робіт. Пересуваючись до останньої події, заповнюють у неї і правий сектор, оскільки 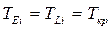. Цим визначена величина критичного шляху. Потім обчислюють Т_Li, послідовно пересуваючись у протилежному напрямі, а саме від події з більшим номером до події з меншим номером, за формулою 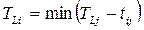, де j – номери всіх наступних подій за кількістю вихідних з події і робіт. У початковій події при цьому повинні отримати 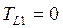, тому що для неї 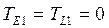. Розташування критичного шляху графіка установлюється, починаючи з завершуваної події, по номерах, що містяться у нижніх секторах.

Після розробки сітьового графіка для календарного планування термінів початку та закінчення робіт складають лінійну діаграму з демонстрацією кількості робіт, що виконуються в кожний момент часу. За допомогою діаграми можна рівномірно розподіляти ресурси часу. Лінійна діаграма являє собою графік, по горизонтальній осі якого відкладається час, по вертикальній – смугами з номерами початкової та кінцевої події – роботи (ті, що розташовані на критичному шляху, заштриховані). Резерви часу для кожної роботи показані штриховими лініями. По результатах діаграми корегується навантаження робіт на бригади та вишукуються можливості їх більш рівномірної роботи, а також скорочення кількості задіяних бригад.

Сітьові графіки використовують також для оптимізації технологічного процесу на сортувальних станціях, який полягає у скороченні тривалості переробки груп вагонів для накопичування їх у поїзди, і відповідно у скороченні тривалості простою вагонів при очікуванні переробки. Важливим напрямком використання сітьових графіків є оптимізація технології обслуговування під’їзних колій навантажувальних станцій з метою зменшення часу простою вагонів.

Але в сучасних умовах підвищених вимог до гнучкості схем роботи залізничних станцій збільшення числа компонентів, що входять до системи, яка проектується, а також ускладнення причинно-наслідкових зв’язків у комплексі компонентів, які взаємодіють, взаємопов’язані та взаємозалежні між собою, описані графи вже не задовольняють цим вимогам.

Останнім досягненням в теорії графів є поява на початку 1960-х років теорії сітей Петрі, які на сучасний момент вже мають широке практичне застосування в багатьох галузях (інформатика, соціологія, хімія, медицина тощо), зокрема, в транспортних системах.