Сітьові задачі управління транспортними системами

Задачі нелінійного програмування є частиною задач класичної оптимізації, які перетворюються в задачі нелінійного програмування, якщо математичну модель задачі складають нелінійні функції. Методи розв’язку задач нелінійного програмування можна класифікувати як прямі та непрямі. Прикладами прямих методів є градієнтні алгоритми, в яких пошук максимуму (мінімуму) в оптимізаційній задачі ведеться у напрямі найшвидшого збільшення (зменшення) значення цільової функції. У непрямих методах початкова задача оптимізації замінюється допоміжною, оптимальний розв’язок якої сприймається як розв’язок початкової. Частковими випадками таких методів є опукле програмування, зокрема квадратичне.

Для предметного розгляду теорії методів розв’язання задач нелінійного програмування наведемо приклад задачі, що приводить до математичної моделі нелінійного програмування.

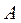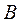Підприємство може випускати два типи виробів та . На їх виготовлення витрачається три типи ресурсів з відомими запасами 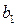, , 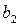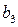. Планові норми витрат ресурсів на одиницю продукції складають 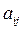од. ( 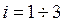, 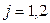). Відомими також у прийнятій методиці розрахунків вважаються планова собівартість виробів 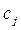та їх оптові ціни 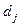( 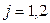). Через наявність браку в процесі виробництва витрати ресурсів залежать від обсягу 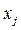( 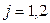) виробництва виробів та в першому наближенні відбиваються лінійною функцією 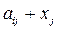, а собівартість продукції - функцією 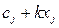, . Вироби можуть випускатися в будь-яких співвідношеннях, оскільки збут їх забезпечений. Необхідно скласти план випуску продукції, який би забезпечив отримання максимального прибутку.

Для складання математичної моделі задачі математичного програмування формалізуємо основну вимогу задачі у вигляді її цільової функції. А саме: від реалізації одиниці виробу 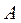підприємство отримає прибуток 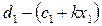грошових одиниць, одиниці виробу 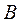- прибуток 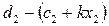гр. од. Загальний прибуток підприємства складе (із зазначенням основної вимоги задачі)

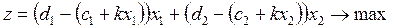. (2.1)

Далі формулюємо обмеження задачі у вигляді системи нерівностей (або рівностей). На виготовлення виробів 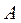та 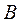, що заплановані підприємством, буде витрачено:

ресурсу І - 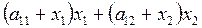одиниць,

ресурсу ІІ - 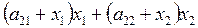одиниць,

ресурсу ІІІ - 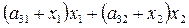одиниць.

Враховуючи обмеженість кількості кожного ресурсу, формалізована система обмежень відбивається системою трьох нерівностей

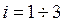, . (2.2)

Додаючи до двох частин постановки задачі природну вимогу невід’ємності складових плану

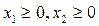, (2.3)

отримуємо повну математичну модель задачі, яка зводиться до знаходження невід’ємних компонент оптимального плану 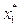, , 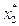які задовольняють нелінійним обмеженням (2.2) та надають максимум нелінійній цільовій функції (2.1).

Типовим прикладом задач, що призводять до математичної моделі нелінійного програмування є задачі управління запасами. Під запасами розуміють той вид продукції, який підлягає збереженню перед його використанням. Таким чином, витрати на створення запасів складаються з витрат на їх виробництво, збереження, а також можливі штрафні санкції за їх нестачу. Основне протиріччя задачі підлягає такому поясненню. При неперервному процесі виробництва, яке є дешевшим, ніж періодичний цикл виробництва з додатковими витратами на зупинку та запуск виробничого процесу, збільшуються витрати на зберігання внаслідок непохитного росту продукції в місцях збереження і відсутності можливості корегування виробництва потребами торгівлі. В протилежному випадку, тобто при випуску продукції партіями різко знижується платня за зберігання, а також зменшується ризик застарілості та втрати конкурентоспроможності продукції, але вартість безпосередньо виробництва зростає. Комплексне дослідження проблеми управління запасами виробило стратегію випуску продукції дискретно, тобто партіями, знаходження оптимального розміру яких і є метою розв’язання задачі управління запасами. Необхідно визначити такі оптимальні розміри випуску запасів продукції, щоб загальні витрати на весь цикл виробництва, зберігання, включаючи можливі штрафи за нестачу, були мінімальними. В загальному випадку такі задачі зводяться до задач нелінійного програмування з різноманітними методами розв’язання [5].

Математична модель загальної задачі нелінійного програмування формується через необхідність знайдення оптимального значення вектора параметрів управління (компонент плану) , який максимізує (мінімізує) цільову функцію

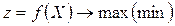(2.4)

і задовольняє 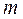обмеженням, кожне з яких може мати один зі знаків , =, , 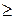тобто

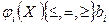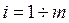, . (2.5)

Припускається, що вигляд всіх функцій відомий, хоча б одна з них є нелінійною. Зазвичай до деяких параметрів управління висувається вимога невід’ємності.

На відміну від лінійних задач, у нелінійних - цільова функція може досягати свого екстремального значення не тільки в її кутових точках, інакше, вершинах (якщо такі точки є) області обмежень або області припустимих розв’язків, але й на межах області та всередині її. Крім того, вона може мати декілька локальних екстремумів. Цим пояснюється відсутність загального методу розв’язання задач нелінійного програмування (ЗНП), подібного симплекс-методу для ЗЛП. Разом з тим для досить поширеного класу ЗНП, а саме задач опуклого програмування, існують достатньо добре розроблені методи розв’язання. Основу математичної моделі опуклого програмування складають опуклі (увігнуті) функції, визначені на опуклих множинах у постановці (2.4)-(2.5).

Опуклою називається множина у векторному просторі, яка разом з будь-якими двома точками містить всі точки відрізку, який їх з’єднує. Аналітично ця властивість опуклої множини описується формулою для радіус-вектора 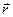поточної точки відрізку через радіус-вектори кінцевих точок відрізку

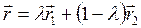, (2.6)

де коефіцієнт .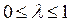

Функція 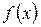, що визначена на опуклій множині, називається опуклою (увігнутою), якщо для будь-яких точок 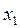та з цієї множини і будь-якого 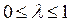вірною є нерівність

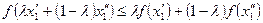(2.7)

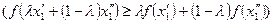. (2.7′)

Порівнюючи формули (2.7) ((2.7′)) з формулою (2.6), можна уявити їх геометричне тлумачення. Нерівність (2.7) ((2.7′)) виражає властивість будь-якої ординати опуклої (увігнутої) функції на відрізку 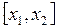приймати менше (більше) значення, ніж ордината хорди, що стягує дугу кривої функції 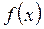(малюнок 2.1, малюнок 2.2). Слід відмітити, що в математичному програмуванні вживають терміни „опуклої” („увігнутої”) функції в протилежному прийнятому в математичному аналізі розумінні.

f(x1" )
Мал. 2.1	Мал. 2.2

Властивості опуклих (увігнутих) функцій:

- якщо функції 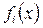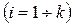є опуклими (увігнутими) на опуклій множині, то опуклою (увігнутою) на цій множині буде лінійна комбінація цих функцій;

- якщо 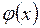- опукла (увігнута) функція при всіх значеннях 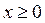, то опуклою буде і множина розв’язків системи , ( , );

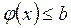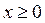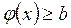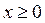- опукла (увігнута) функція 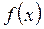, що визначена на опуклій множині, досягає свого глобального мінімуму (максимуму) в кожній точці 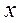, в якій градієнт функції обертається в нуль;

- локальний мінімум (максимум) опуклої (увігнутої) функції на опуклій множині збігається з її глобальним мінімумом (максимумом) на цій множині.

Серед можливих методів розв’язання задачі опуклого програмування для двовимірних задач виділяють графічний метод, який, як і для задач лінійного програмування передбачає геометричний спосіб знаходження оптимального рішення. В опуклій області, що є геометричним образом системи обмежень задачі (2.5), знаходиться точка, через яку проходить геометричний образ цільової функції (2.4) - лінія рівня поверхні - і координати якої відповідають максимальному (мінімальному) значенню цільової функції. Як відомо, рівняння сім’ї ліній рівня задається рівністю

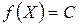, (2.8)

де 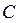- довільне стале значення.

Приклад 2.1. Знайти екстремальні значення функції 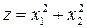в області невід’ємних розв’язків системи нерівностей, тобто математична модель задачі має такий вигляд

;

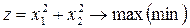1. Графічний образ системи нерівностей – область, що обмежена відрізком 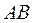прямої , дугою 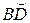кола 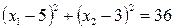з центром у точці (5;3) радіуса 6 та відрізком осі 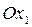- 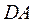(малюнок 2.3).

2. Сім’я ліній рівня - сукупність концентричних кіл з центром 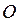, що міститься в початку координат.

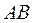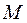3. Визначаємо точку мінімуму функції як точку дотику кола лінії рівня з відрізком межі - т. , координати якої знаходимо як точку перетину відрізка 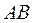та перпендикулярного йому радіуса 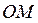, рівняння якого формуємо як канонічне рівняння прямої через т. 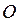у напрямі нормального до прямої 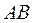вектора :

.

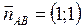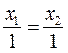Розв’язуємо систему рівнянь

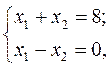
отримуючи координати точки мінімуму цільової функції 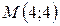. Отже,

.

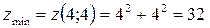Точку максимуму цільової функції фіксуємо як останню точку дотику кола із сім’ї ліній рівня з областю припустимих розв’язків – т. 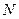, координати якої визначаємо як точку перетину кола з системи обмежень та прямої 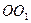, яка описується рівнянням прямої, що проходить через дві точки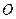 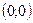та 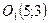. Складаємо та розв’язуємо систему рівнянь для знаходження т.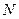

; ;

; ;

.

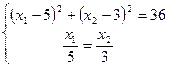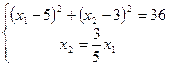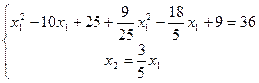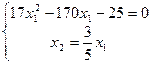Розв’язуючи квадратне рівняння, обираємо додатний корінь. Таким чином знаходимо координати точки 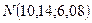, а також відповідне значення цільової функції задачі на максимум

.

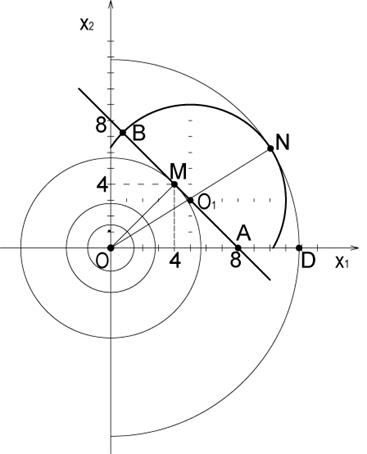
Мал. 2.3

Серед задач опуклого програмування виділяють частковий випадок таких задач - задачі квадратичного програмування. В таких задачах цільова функція містить квадратичні доданки, а обмеження - лінійні. Приклади розв’язання таких задач графічним методом наведені в методичних вказівках [3], [4].

Розвинення логіки розв’язання задач опуклого програмування аналітичними методами будується, починаючи з простішого випадку постановки задачі на умовний екстремум. Якщо серед обмежень (2.5) немає нерівностей, умов невід’ємності та дискретності змінних, 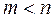, а функці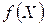ї і 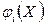неперервні та мають частинні похідні хоча б другого порядку, то задача приводиться до вигляду

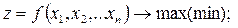(2.9)

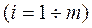. (2.10)

Такі нелінійні задачі називають класичними задачами оптимізації , і для їх розв’язання використовують метод множників Лагранжа. Головною ідеєю цього методу є перехід до задачі на безумовний екстремум відносно функції Лагранжа, яка включає в себе безпосередньо цільову функцію (2.9) та систему обмежень (які ще називають рівняннями зв’язку) з так званими ваговими коефіцієнтами або множниками Лагранжа 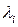( 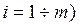. Отже, функція Лагранжа є функцією двох типів змінних: компонент вектора параметрів управління (компонент плану) задачі та компонент вектора множників Лагранжа 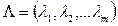- і має вигляд

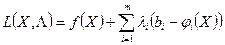. (2.11)

Далі, як для задачі на безумовний екстремум, знаходять стаціонарні точки функції Лагранжа з системи рівнянь, які відбивають необхідні умови існування екстремуму

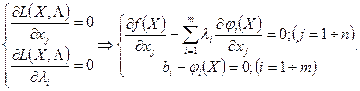(2.12)

Наступним кроком із стаціонарних точок без значень 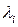, обирають такі, в яких функція 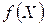має умовні екстремуми з урахуванням обмежень (2.10). Цей відбір здійснюють, наприклад, за допомогою достатніх умов існування екстремуму, але при розв’язанні конкретних задач дослідження спрощується за рахунок використання штучних прийомів, що прийняті за методику обчислень.

У методичних вказівках [5] описані методи розв’язання задач управління запасами в рамках постановки класичної задачі оптимізації з використанням спеціальних прийомів, що придатні саме для таких задач.

Метод множників Лагранжа узагальнюється на випадок, коли в математичній моделі (2.4)-(2.5) змінні невід’ємні та деякі обмеження задані у формі нерівностей. Суть методу полягає в тому, що для математичної моделі

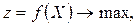(2.13)

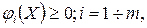(2.14)

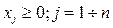(2.15)

створюється функція Лагранжа

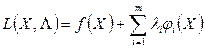, (2.16)

необхідні умови існування екстремуму для якої мають вигляд умов Куна-Таккера. Вони використовуються для знаходження так званої сідлової точки функції Лагранжа 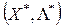, яка визначається як така, що задовольняє ланцюжку нерівностей

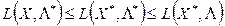. (2.17)

Ця формула виражає основну властивість сідлової точки бути одночасно точкою мінімуму функції відносно вектора однієї змінної та точкою максимуму відносно вектора іншої.

За теоремою Куна-Таккера доводиться, що при виконанні деяких умов вектор є оптимальним розв’язком задачі (2.13)-(2.15) тоді і тільки тоді, коли для нього можна вказати значення вектора 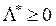таке, що у сукупності ці вектори створюють сідлову точку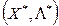 функції Лагранжа (2.17). Практично теорема Куна-Таккера зводиться до умов Куна-Таккера для знаходження сідлової точки

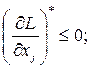
; (2.18)

.

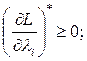
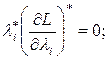
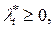
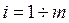Приклади, які поєднують використання графічного методу розв’язання задачі квадратичного програмування та умов Куна-Таккера для знаходження сідлової точки цієї задачі, детально розглянуті в методичних вказівках [3], [4].

Градієнтні методи можна застосовувати для розв’язання будь-якої задачі нелінійного програмування, але вони приводять лише до локального екстремуму. І знов особливе місце серед ЗНП займають задачі опуклого програмування, для яких кожний локальний екстремум є одночасно і глобальним.

Градієнтні методи використовують властивість вектора-градієнта (антиградієнта) функції, координати якого в даній точці визначаються частинними похідними функції в цій точці, визначати напрям найшвидшого зростання (спадання) цієї функції, тобто для функції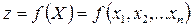

. (2.19)

Для опуклої функції необхідною та достатньою умовою оптимальності точки 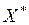є рівність нулю градієнта функції в цій точці.

Алгоритм пошуку екстремуму функції 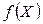організований так. У припустимій області розв’язків обирається довільна точка 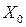та за допомогою градієнта (антиградієнта) визначається напрям, у якому зростає (спадає) з найбільшою швидкістю. Зробивши певний невеликий крок у знайденому напрямі, переходимо до наступної точки 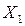. Процес повторюється доти, поки не відбудеться збігання до точки екстремуму 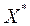, тобто для послідовності точок 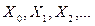необхідне виконання умов 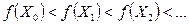в задачі на максимум ( - в задачі на мінімум).

Величина кроку, наприклад, з точки 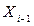до точки в напрямі градієнта (антиградієнта 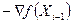) визначається величиною параметра у рівнянні прямої

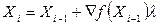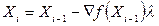( ), (2.20)

що проходить через точку 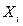паралельно градієнту (антиградієнту). Значення обирають або з конкретних умов задачі, або з таких міркувань: переміщення уздовж прямої (2.20) до нової точки супроводжується зміною функції на величину

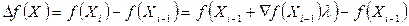, (2.21)

яка залежить від обраного значення . Можна знайти оптимальне значення , яке надає приросту функції 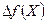найбільшої величини. Це значення можна знайти з необхідних умов існування екстремуму

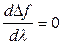
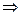
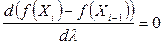
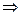
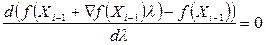
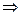
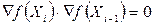. (2.22)

Приклад 2.2. Максимізувати функцію

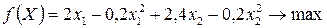
при наявності обмежень

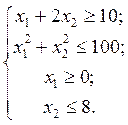
Обираємо у припустимій області рішень довільну точку, наприклад, , яка дійсно належить області обмежень, що можна перевірити простою підстановкою:

- вірно;

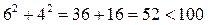- вірно;

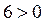- вірно;

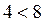- вірно.

Знаходимо

.

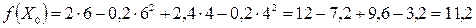Обчислюємо координати градієнта

,

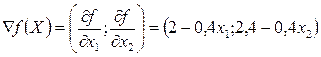і тоді в точці 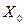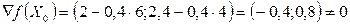, тобто точка 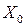не є точкою екстремуму.

Знайдемо рівняння прямої, уздовж якої перемістимося до нової точки 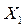у напрямі градієнта, за формулами (2.20) для кожної координати точки 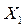, а саме

.

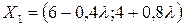Для визначення координат точки 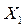скористуємося умовами (2.22) для знаходження значення . Для цього сформуємо вираз для :

.

І тоді, записуючи необхідні умови існування екстремуму (2.22), отримаємо рівняння відносно параметра :

.

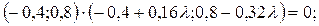
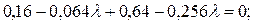
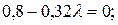
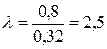Тобто, координати точки 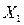такі: 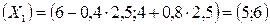, причому вона належить області обмежень (в чому легко переконатися перевіркою вірності нерівностей у системі обмежень). Перевіряємо значення градієнта функції в цій точці

.

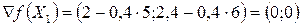Це означає, що більш ніякими переміщеннями не можна збільшити функцію , і тому 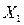- точка максимуму . Отже,

, .

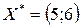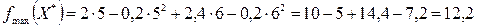Розв’язок задачі проілюстровано на малюнку 2.4.

Треба відмітити, що у розглянутому прикладі точний розв’язок отриманий за кінцеву кількість кроків (що зокрема відбулося за рахунок вдалого обрання початкової точки), але, як правило, градієнтні методи дають точний розв’язок за нескінченну кількість кроків.

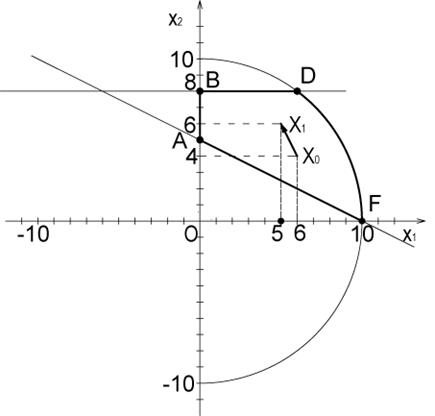
Мал. 2.4

Сітьові задачі управління транспортними системами

4.1. Елементи теорії графів

Для завдання графів використовується два типи множин: множина вершин графа

,

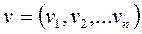та множина ребер або дуг графа

.

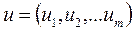Кожний елемент 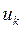( 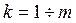) визначається певною парою вершин, які він поєднує, тобто

.

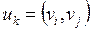Отже, граф – це і є сукупність пар елементів 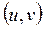. Первинним, а тому невизначеним, є поняття вершини, яке можна розуміти як деякий „вузол”, який позначається крапкою, кільцем, квадратом або трикутником. В залежності від типу графа: графа станів або географічного - вузол може означати стан, умову або пункт призначення. В першому випадку граф являє собою зображення процесу зміни станів об’єкта, у другому – граф будується подібним до „географії” об’єкта, що моделюється. Ребра або дуги – це відрізки прямих або кривих, які з’єднують вершини. Послідовність ребер утворює ланцюг. Ребро 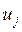називається інцидентним вершині 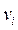, якщо воно входить або виходить з цієї вершини. Степінь (валентність) вершини – кількість інцидентних до неї ребер. Граф називається орієнтовним або орграфом, якщо вказано, яка вершина є початковою, тобто показаний напрям дуг. Якщо з кожним ребром графа пов’язані якісь числові характеристики, або інакше - ребрам графа приписана певна вага, то граф називається зваженим. Кожному графу можна поставити у відповідність квадратну матрицю суміжності, розмір якої визначається кількістю вершин і яка складається з елементів 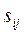, що дорівнюють сумі чисел орієнтованих або неорієнтованих ребер, які поєднують вершини 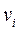та 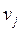. Важливим поняттям в теорії графів є поняття зв’язності графа, яке пов’язане з наявністю принаймні одного шляху для будь-яких двох вершин графу. Граф називають петлею, якщо його початок і кінець збігаються. Циклічним називають граф, який являє собою кінцевий ланцюг, у якого збігаються початкова і кінцева вершини. Ще деякі відомості про графи на початковому рівні можна брати з методичних вказівок №№ 3535, 1441.

Взагалі, графи, як інструмент моделювання, мають дуже широке використання саме у транспортних задачах, завдяки таким достоїнствам, як наочність, гнучкість апарата. Розглянемо спочатку деякі з найбільш традиційних сітьових задач.