Гармонічні коливання та їх основні параметри
Розглянемо пружинний маятник (мал. 1.21). При зміщенні матеріальної точки масою т на відстань х відносно положення рівноваги на неї починає діяти сила пружності, яка викликана деформацією пружини
Fnp = -kx. (1.35)
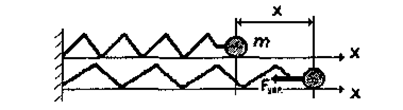
Мал. 1.21. Пружинний маятник.
Згідно з II законом Ньютона ця сила надаватиме матеріальній точці прискорення :
Fnp = ma. (1.36)
Прирівнюючи праві частини рівностей (1.35) і (1.36), одержимо:
ma = -kx. (1.37)
Враховуючи, що прискорення є другою похідною від координати за часом a = х, останнє рівняння набуває вигляду лінійного диференційного рівняння
m 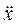 +kx=0. (1.38)
+kx=0. (1.38)
Оскільки коефіцієнт жорсткості пружини k > 0 і т > 0, відношення k/m можна позначити через квадрат деякої величини ω0: ω02=k/m. Тоді рівняння (1.38) матиме вигляд:
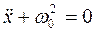 . (1.39)
. (1.39)
Таким чином, функція х =f(t) задовольняє диференційному рівнянню ІІ-го порядку, яке є лінійним, однорідним і зі сталими коефіцієнтами. Розв'язок таких рівнянь, як відомо, зводиться до розв'язування відповідних характеристичних алгебраїчних рівнянь.
Складемо характеристичне рівняння, що відповідає ди-ференційному рівнянню (1.39):
λ2+ω02=0. (1.40)
Корені цього квадратного рівняння дорівнюють λ1,2 = ±ω0 , тобто вони є різними й уявними.
Загальний розв'язок диференційного рівняння (1.39) на випадок таких коренів відповідного характеристичного рівняння має вигляд:
x(t) = с1 sinω0t + с2 cosω0t.
Нехай с1 = Acosφ0, а с2 = - А sinφ0, де А та φ0 - довільні сталі, тоді
x(t) = Acosφ() cosω0t- Asinφ sinωt= Acos(ω0t + φ0). (1.41)
Якщо покласти с1 = A sinφ0, а с2 = А cosφ0, то прийдемо до результату:
x(t) = Asin(ω0t + φ0). (1.42)
Значення сталих А та φ0 визначаються початковими умовами, тобто положенням та швидкістю матеріальної точки в момент часу t = 0.
Отже, ми дійшли до висновку: матеріальна точка, що знаходиться під дією пружної сили, здійснює коливальний рух, при якому її зміщення від положення рівноваги змінюється з часом за законом синуса або косинуса. Такі коливання називають гармонічними.
Стала А в рівняннях (1.42) є амплітуда гармонічного коливання, вона дорівнює максимальному зміщенню маятника від положення рівноваги. Аргумент синуса (або косинуса): φ(t) = ω0t + φ0 - фаза коливань. Фаза визначає зміщення маятника в будь-який момент часу, φ0- початкова фаза, яка визначає зміщення маятника в момент часу t = 0.
Величина ω0= 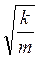 - циклічна частота коливань.
- циклічна частота коливань.
Тій же самій закономірності підпорядковується зміщення від положення рівноваги математичного маятника, що коливається, при невеликих кутах відхилення а (мал. 1.22).
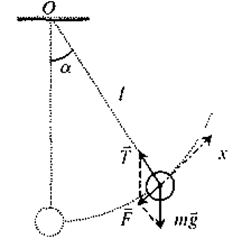
Мал. 1.22. Математичний маятник.
Сила, яка спричиняє коливання математичного маятника, не є пружна за своєю природою. Дійсно, повертаюча сила F спрямована по дотичній до дуги кола радіуса l, напрямлена до положення рівноваги і пропорційна зміщенню х:
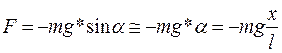
(оскільки для малих кутів α маємо 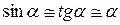 ).
).
Сила, що не є пружною за своєю природою, але аналогічна їй по залежності від зміщення, називається квазіпружною. Таким чином, F є квазіпружною силою. Рівняння динаміки для математичного маятника матиме вигляд:
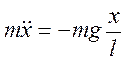 , або
, або 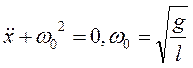 (1.43)
(1.43)
Отримане рівняння повністю збігається з рівнянням (1.41), що описує рух пружного маятника, а отже має той самий розв'язок. Таким чином, гармонічні коливання - це коливання, що відбуваються під дією пружних або квазіпружних сил.
Швидкість та прискорення при гармонічних коливаннях
Нехай відлік часу обрано таким чином, щоб початкова фаза φ0= 0. Тоді розв'язок рівняння (1.41) матиме вигляд:
x(t) = Asinω0 t. (1.44)
Швидкість тіла, що коливається, знайдемо як похідну від координати х за часом t
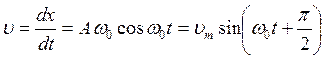 , (1.45)
, (1.45)
де υm = aω0 - амплітуда швидкості.
З рівнянь (1.43) та (1.44) випливає, що швидкість також змінюється за гармонічним законом, а фаза швидкості відрізняється від фази зміщення на π/2, тобто в момент часу, коли х = 0, швидкість максимальна.
Оскільки швидкість при гармонічних коливаннях змінюється з часом, то цей рух характеризується прискоренням, яке знайдемо як другу похідну від зміщення х за часом
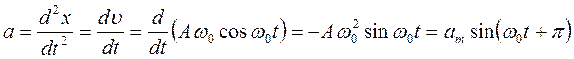 (1.46)
(1.46)
де ат = Аω02 - амплітуда прискорення.
Видно, що і прискорення змінюється за гармонічним законом, а фаза прискорення відрізняється від фази зміщення на π, а від фази швидкості на π/2. Замінивши в (1.46) Asinω0t через х, отримаємо:
a=-ω02x.
З цієї рівності виходить, що при гармонічних коливаннях прискорення тіла прямо пропорційне до зміщення від положення рівноваги і має протилежний зміщенню напрямок.
Період і частота гармонічних коливань
Періодом гармонічного коливального руху називають найменший проміжок часу Т, по закінченні якого всі величини, що характеризують цей рух (х, υ, а), набувають первісні значення. З рівностей (1.44) - (1.46) випливає, що періоду коливань відповідає зміна фази на величину 2π.
У момент часу t фаза дорівнює ω0t+φ0, а в момент часу t + Т: (ω0 (t + T) +φ0 ). Тоді з умови періодичності (ω0 (t + T) +φ0)- -( ω0t+φ0 )= 2π маємо:
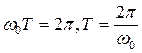 . (1.47)
. (1.47)
Підставляючи в (1.47) вирази для ω0, що відповідають пружинному та математичному маятникам, отримаємо відповідні вирази для періодів коливань цих маятників:
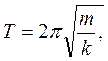
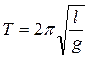 (1.48)
(1.48)
Величину v=1/Т = ω0/2π називають частотою коливань. Частота вказує, скільки разів за 1 сек повторюється один і той же стан тіла, що коливається. Частота вимірюється в Герцах (Гц), [v] = 1/с = с-1 = Гц.
Розглянуті коливання відбуваються при відсутності сил тертя і зовнішніх сил. Такі коливання називають власними. Частота (період) власних коливань, як випливає з (1.48), залежить лише від властивостей самої системи.
Дата добавления: 2015-03-03; просмотров: 3903;
