Вимушені коливання

Припустимо, що на матеріальну точку масою m, крім пружної або квазіпружної сили і сили тертя, діє зовнішня вимушуюча сила, що змінюється за періодичним законом

F₃ = F₀sin Ωt,

де F₀ - амплітуда, а Ω - циклічна частота вимушуючої сили. В цьому випадку рівняння руху матиме вигляд

ma = - kx - r 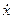+ F₀sinΩlt, або

. (1.53)

Загальний розв'язок диференційного рівняння (1.53) має вигляд

х = Asin(Ωt + φ₀), (1.54)

де А - амплітуда вимушених коливань, яка дорівнює

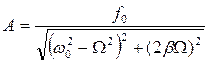, (1.55)

а початкову фазу φ₀ визначають з рівності:

. (1.56)

Важливу формулу (1.55) для амплітуди А вимушених коливань можна отримати, скориставшись графічним мето­дом розв'язку неоднорідних диференційних рівнянь 2-го порядку з постійними коефіцієнтами. З формули (1.54) для зміщення х легко отримати вирази для похідних

Якщо намалювати "векторну" або "фазову" діаграму (мал. 1.25а), відклавши на ній амплітудні значення всіх доданків у рівнянні (1.53) з урахуванням зсуву їх фаз, то очевидно, що векторна сума трьох доданків у лівій частині (1.53) повинна дорівнювати амплітудному значенню виму­шуючої сили, тобто 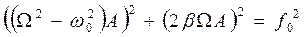. Звідси безпосередньо випливає формула (1.55) для амплітуди А, так само як і формула (1.56) для tgφ.

Мал. 1.25а. Векторна діаграма для визначення амплітуди А і початкової фази φ₀.

Таким чином, якщо на тіло, яке коливається, діє зовнішня періодична сила з частотою Ω, то тіло здійснює коливання з тією ж частотою, причому амплітуда коливань залежить від амплітуди і частоти зовнішньої сили, від коефіцієнта затухання, від пружних властивостей системи і маси тіла, яке коливається. Такі коливання називають вимушеними.