Оптимальная смесь стратегий.
Итак, запишем, каковы будут издержки в случае, если реализовать все три стратегии сразу:
нанимать и увольнять рабочих;
назначать сверхурочные и незанятые часы;
отправлять излишки продукции на склад и забирать их со склада.
Сводя все рассмотренные ранее формулы для расходов, получим

В этой формуле 6 переменных, каждая в 12 экземплярах (по числу месяцев в году). Однако, разумеется, не все переменные являются независимыми. Запишем известные связи между ними.
Во-первых, выражение для количества имеющихся в распоряжении нормированных рабочих часов 

Понятно, что количество имеющихся рабочих часов зависит от числа рабочих в компании в данном месяце 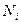 . Однако это число непосредственно не входит в выражение для суммарных издержек. Выразим его через количество нанятых и уволенных рабочих в данном месяце:
. Однако это число непосредственно не входит в выражение для суммарных издержек. Выразим его через количество нанятых и уволенных рабочих в данном месяце:

Здесь отражен следующий простой факт: количество рабочих в данном месяце равно количеству рабочих в предыдущем месяце плюс количество рабочих, нанятых в начале данного месяца, минус количество рабочих, уволенных в начале данного месяца. Разумеется, что в каждом месяце рабочие либо нанимаются, либо увольняются, т.е. одна из двух величин 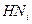 или
или  всегда равна нулю. Тем не менее, удобно ввести обе эти величины. Они выражают собой первую пару независимых переменных для каждого месяца.
всегда равна нулю. Тем не менее, удобно ввести обе эти величины. Они выражают собой первую пару независимых переменных для каждого месяца.
Действительно, сколько нанять и сколько уволить рабочих в данном месяце – это управленческое решение, совершенно независимое от предыстории. Следить же за тем, чтобы одна из этих величин равнялась нулю, поручается Поиску решения. Минимизируя суммарные издержки, алгоритм Поиска решения не должен позволить обеим этим величинам быть отличным от нуля в одном и том же месяце. Это неоправданно увеличит издержки.
Обратимся теперь к выражению для стоимости остатка продукции на складе 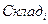 . Это выражение дается формулой:
. Это выражение дается формулой:
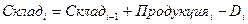
где, однако, выражение для произведенной продукции должно быть теперь изменено по сравнению со старой формулой 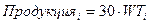 . Ведь теперь, продукция производится не только в нормированные часы
. Ведь теперь, продукция производится не только в нормированные часы  , но и в сверхурочные часы
, но и в сверхурочные часы 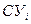 , и не производится в незанятые часы
, и не производится в незанятые часы  . Таким образом,
. Таким образом,
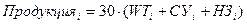
Теперь видно, что остаток на складе и произведенная продукция могут быть выражены через уже введенные переменных 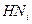 и
и  и через новую пару переменных решения
и через новую пару переменных решения 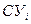 и
и  . Опять очевидно, что количество назначенных в данном месяце сверхурочных и незанятых часов – это независимое управленческое решение. Как и в случае первой пары переменных, в этой паре одна из переменных в каждом данном месяце должна быть равна нулю. И опять возлагается контроль выполнения этого требования на Поиск решения. Он обеспечит его выполнение из соображений минимума полных издержек.
. Опять очевидно, что количество назначенных в данном месяце сверхурочных и незанятых часов – это независимое управленческое решение. Как и в случае первой пары переменных, в этой паре одна из переменных в каждом данном месяце должна быть равна нулю. И опять возлагается контроль выполнения этого требования на Поиск решения. Он обеспечит его выполнение из соображений минимума полных издержек.
Итак, в решаемой задаче линейной оптимизации должно быть 4 независимых переменных каждый месяц. Всего – 48 переменных.
Сформулируем ограничения. Единственное неформальное ограничение, которое необходимо выполнить, минимизируя годовые издержки, это обеспечить безусловное выполнение плана отгрузки продукции потребителям.
Это не значит, что каждый месяц нужно производить столько продукции, сколько требуется отгрузить или больше. Как следует из стратегии №3, это значит, что остаток на складе в каждом месяце не должен опускаться ниже нуля.
Реально на с кладе, разумеется, не может быть отрицательного количества продукции, но в формуле 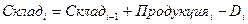 , этот остаток вполне может стать отрицательным, если произведенной в данном месяце продукции плюс запаса на складе окажется меньше значения потребительского спроса
, этот остаток вполне может стать отрицательным, если произведенной в данном месяце продукции плюс запаса на складе окажется меньше значения потребительского спроса 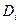 . Чтобы не допустить этого, достаточно потребовать в ограничениях Поиска решения, что остаток на складе в каждый месяц был неотрицательным, т.е.
. Чтобы не допустить этого, достаточно потребовать в ограничениях Поиска решения, что остаток на складе в каждый месяц был неотрицательным, т.е. 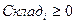 при всех значениях i от 1 до 12.
при всех значениях i от 1 до 12.
Рассмотрим ограничения на сверхурочные часы. Исходя из обычной практики, ограничим число сверхурочных в месяц 20% от числа нормированных часов, т.е. запишем, что 
На Рис.8 показана организация данных для решения задачи линейной оптимизации. Переменные решения – ячейки D5:G16. В ячейке H5 – выражение для количества рабочих в январе. В ячейках H6:H16 введено выражение для количества рабочих в компании  для каждого месяца, начиная с февраля. С этого месяца формулу можно протягивать. В ячейках I5:I16 введена формула
для каждого месяца, начиная с февраля. С этого месяца формулу можно протягивать. В ячейках I5:I16 введена формула  для количества рабочих часов, в ячейках J5:J16 – формула
для количества рабочих часов, в ячейках J5:J16 – формула 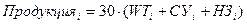 для количества произведенной продукции.
для количества произведенной продукции.
В ячейках K5:K16 записана формула 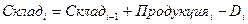 для остатков продукции на складе. Так же как и в случае с числом рабочих, ее можно протягивать, начиная со второго месяца. Поэтому формулы в ячейках K5 и K6:K16 отличаются. В ячейках L5:L16 введено выражение для ежемесячных издержек, в соответствие с итоговой формулой, а в ячейке L17 – сумма этих издержек – наша целевая функция. Последняя колонка, ячейки M5:M16 – это максимальное значение сверхурочных часов каждый месяц, необходимое для ввода ограничений.
для остатков продукции на складе. Так же как и в случае с числом рабочих, ее можно протягивать, начиная со второго месяца. Поэтому формулы в ячейках K5 и K6:K16 отличаются. В ячейках L5:L16 введено выражение для ежемесячных издержек, в соответствие с итоговой формулой, а в ячейке L17 – сумма этих издержек – наша целевая функция. Последняя колонка, ячейки M5:M16 – это максимальное значение сверхурочных часов каждый месяц, необходимое для ввода ограничений.
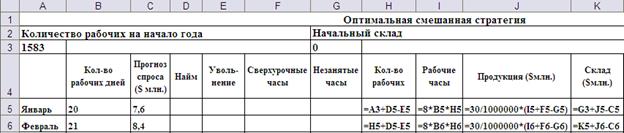

Рис.8. Структура таблицы и ввод формул для расчёта издержек при Оптимальной смешанной стратегии.
В ограничениях Поиска решений вводится требование, чтобы ячейки K5:K16 были бы не меньше нуля (склад не должен быть отрицательным) и F5:F16 не больше, чем M5:M16 – ежемесячные сверхурочные не превышают 20% от нормированных часов в данном месяце. На Рис. 9 показано решение, полученное после запуска надстройки Поиск решения.

Рис.9. Результаты расчёта издержек при Оптимальной смешанной стратегии.
Во-первых, отметим, что суммарные издержки в оптимальной смешанной стратегии примерно на $1172886 ниже, чем в третьей, лучшей из чистых стратегий. Во-вторых, сам план управления трудовыми ресурсам и запасами на складе выглядит намного привлекательнее, чем в чистых стратегиях.
Действительно, если сравнить суммарный объем продукции, лежащей на складе в течение года, согласно смешанной и чистой стратегиям (т.е. просуммировать числа в ячейках K5:K16 (Рис.9) и E4:E15 (Рис.7) ), то окажется, что в смешанной стратегии эта сумма равна $11,8 млн., а в чистой $87,8 млн.
Еще более заметно преимущество смешанной стратегии в управление трудовыми ресурсами. Действительно, вместо огромных чисел нанятых и уволенных рабочих и больших количеств сверхурочных часов в стратегиях №1 и №2, смешанная стратегия рекомендует нанять 1102 рабочих (сумма ячеек D5:D16), никого не увольнять, не назначать сверхурочных, и в декабре предоставить рабочим ~40803 незанятых часов, которые составляют менее 10% от нормированных рабочих часов декабря.
После первого впечатления от «сказочной» эффективности метода линейной оптимизации, возникают, однако некоторые вопросы.
Вопрос 1. Полученное решение рекомендует нанять 1102 рабочих. Это значит, что следующий год компания начнет не с 1583 рабочими (как нынешний), а с 2685 рабочими. Допустим, что следующий год будет таким же, как предыдущий (тот же объем и та же сезонность спроса). Какой план получится по этой смешанной стратегии? Что делать с 1130 нанятыми рабочими?
Ответ на этот вопрос получить совсем нетрудно. Для этого достаточно просто поменять число рабочих в начале года с 1583 на 2685 и вызвать Поиск решения еще раз. Новое решение показано на Рис.10.
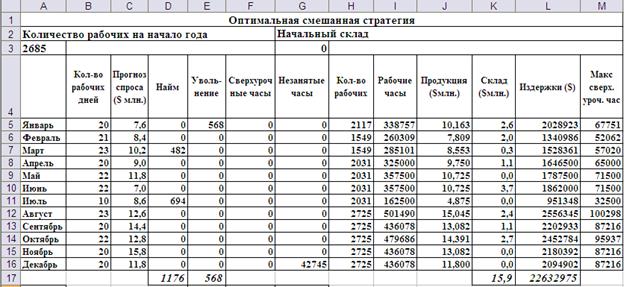
Рис.10. Вариант расчёта издержек при Оптимальной смешанной стратегии.
Полные издержки возросли на $ 38730 , но они, все равно остаются на ~$1,17 млн. ниже, чем в лучшей из чистых стратегий. Что же происходит с планом управления трудовыми ресурсами? Полученное решение рекомендует уволить 568 рабочих в январе и нанять 1176 рабочих (в марте и июне). Таким образом, опять нанял на 608 человек больше, чем уволил. Численность рабочих в компании возросла до 3293 человек. Интересно, этот процесс когда-нибудь остановится? Чтобы проверить это, необходимо повторить процесс многократно, каждый раз увеличивая начальную численность рабочих на величину разности между нанятыми и уволенными. Результаты повторных расчётов сведены в таблицу:
| № | Начальная численность рабочих | Численность нанятых рабочих | Численность уволенных рабочих | Рекомендованная начальная численность на следующий год | Издержки ($) |
| 567,77 | |||||
| …… | …… | …… | …… | …… | |
Итак, на восьмой итерации получили равенство принятых и уволенных рабочих. Таким образом, процесс вышел на стационарный режим. Стационарное решение показано на Рис.11.

Рис.11. Стационарный вариант расчёта издержек при Оптимальной смешанной стратегии.
Задумаемся над полученным результатом. Фактически, модель дает рекомендации относительно желательной численности структуры наших трудовых ресурсов. Если предстоящий нам год – типичный по объему заказов их распределению по месяцам, то для минимизации издержек нам следует иметь не 1583 рабочих, а 3968, причем 1300 должны быть сезонными рабочими.
Подобный вопрос не ставился, когда формулировалась задача среднесрочного планирования. Но в этом, как раз, и сила хорошей количественной модели: она содержит в себе ответы количественной модели: она содержит в себе ответы на вопросы, которые мы даже не предполагали задавать при ее формулировке.
Вопрос 2. Не слишком ли малы изменения издержек в разных рассмотренных стратегиях? Ведь фактически, при суммарных издержках на уровне $22-25 млн. разница между различными стратегиями (включая оптимальную) не превышает $1-2 млн. Стоит ли вообще тратить время на минимизацию?
Для ответа на этот вопрос рассчитаем, сколько нужно выплатить рабочим за нормированные часы, чтобы выполнить годовой план по спросу. Просто просуммируем цифры ежемесячных спросов в ячейках C5:C16 последней таблицы, умножим на 1 млн., разделим на 30 и умножим на стандартную оплату одного рабочего часа - $5. Получится $21,7 млн. Это – тот базовый уровень неизбежных расходов, от которого и нужно отсчитывать реальные издержки, связанные с тем, что план отгрузки нужно выполнять каждый месяц (а не только в целом за год), для чего необходимо варьировать численность рабочих, сверхурочных и незанятых часов и нести издержки хранения.
Если использовать этот базовый уровень неизбежных затрат, то нетрудно проверить, что оптимальная стратегия лучше, чем стратегия №1 – в 1,8 раза, чем стратегия №2 – в 2,3 раза, чем стратегия №3 – в 1,2 раза.
Кроме того, время даже очень квалифицированного сотрудника, затраченное на подобную минимизацию стоит гораздо меньше, чем $1 млн.
Вопрос 3. Зачем компьютер в декабре вводит режим неполной занятости, если в январе следующего года рабочих, все равно, придется увольнять?
Этот вопрос «индуцирован» процедурой исследования, проведенной при ответе на вопрос 1. Там мы, как бы, свернули нашу таблицу MS Excel в кольцо, оптимизируя план на несколько идентичных лет вперед. Реально, компьютер оптимизирует план от января до декабря и ничего «не знает» про следующий январь. Следующий год – за границами нашей модели.
Вопрос 4. Почему, все-таки, компьютер не использует сверхурочных часов? Ответ на этот вопрос очевиден: потому что ставка оплаты за сверхурочные часы слишком высока по сравнению с другими имеющимися возможностями.
Таким образом, опять, анализ агрегатного плана оптимальной смешанной стратегии стимулирует обсуждение вопросов, выходящих за рамки среднесрочного планирования. Если мы хотим уменьшить число сезонных рабочих, рекомендованное по результатам анализа вопроса 1, следует пересмотреть тариф оплаты сверхурочных часов.
Дата добавления: 2015-02-19; просмотров: 998;
