Системы с последовательным, параллельным и смешанным соединением элементов.

В теории надежности различают системы с последовательным, параллельным и смешанным соединением элементов.

Последовательным соединением элементов в системе называется такое соединение, в котором отказ одного элемента вызывает отказ всей системы (конструкции). Классическим примером последовательного соединения элементов в системе является статически определимая стропильная ферма, где при отказе одного из элементов (нижнего или верхнего пояса, стойки, раскосов, узловых соединений) конструкция выходит из строя.

Предварительно напряженную железобетонную балку можно рассматривать как систему, состоящую из звеньев, соединенных последовательно (рис. 29.1).

Отказ такой системы может произойти в результате разрушения по нормальному сечению среднего звена, излома по наклонному сечению крайнего звена или проскальзывания предварительно напряженной арматуры.

Модели систем последовательно соединенных элементов мо­гут быть использованы в расчетах надежности следующих конст­рукций: перекрытия и покрытия из свободно опертых балок и балоч­ных плит, самостоятельных колонн и стен и других статистически определимых систем.

Рис.29.1. Последовательное соединение звеньев железобетонной балки; Р₁, Р₂, Р₃ – показатели надежности звеньев.

При последовательном соединении по связи с другими отка­зами могут возникать независимые и зависимые отказы. В том слу­чае, если элементы подвергаются воздействию общих возмущаю­щих факторов, их отказы полностью зависимы. Например, тяжелые железобетонные конструкции с целью уменьшения массы монтажных элементов расчленяют на отдельные блоки, которые затем объединяют в целую конструкцию предварительным напря­жением арматуры. Каждый блок и стык между блоками представля­ют собой отдельный элемент, соединенный с двумя другими смежны­ми элементами последовательно. При натяжении арматуры, усилие от которой воспринимается всеми элементами, отказ может произойти по наиболее слабому звену (слабый блок или стык), надежность такой системы (конструкции) Р_с равна надежности наименее сла­бого элемента Р_t,min:

Р_с = Р_t,min (29.1)

При независимых отказах разрушение одного элемента системы не связано с отказами других элементов. Например, сборный ригель междуэтажного перекрытия может выйти из строя в связи с исчерпанием прочности в одном из опасных сечений ригеля или из-за отказа в узловых соединениях на колоннах. Оба случайных события (исчерпание прочности ригеля и отказ узловых соединений) являются взаимно независимыми.

Безотказная эксплуатация системы из последовательно соединенных элементов есть случайное событие, а показатель надежности — вероятность безотказной работы системы при независимых отказах с последовательным соединением элементов определяется перемножением соответствующих вероятностей:

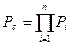(29.2)

где n — число элементов системы (конструкции).

С увеличением числа элементов надежность системы с последовательным соединением элементов быстро убывает. Однако она не должна превышать надежности наиболее слабого элемента:

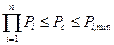
Если известна корреляционная связь между отказами элементов, то при линейной зависимости между вероятностями безотказной работы конструкции надежность системы

Р_с = Р_нез + r(P_i,min - P_нез), (29.3)

или

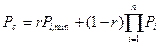(29.4)

где 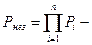вероятность безопасной эксплуатации при независимых отказах

r - обобщенный коэффициент корреляции между вероятностями зависимых и независимых отказов системы.

Надежность конструкций с последовательным соединением элементов увеличивается не только повышением вероятности рабо­тоспособности отдельных элементов и стохастической связи между ними, но и путем уменьшения числа расчетных элементов в системе за счет стыковых соединений.

Для определения надежности системы необходимо провести анализ конструктивной схемы здания и сооружения и установить характер связи между отказами отдельных элементов. Если отказы практически независимы, то надежность конструкции следует опре­делять по формуле (29.2), при наличии существенной зависимости отказов элемента—по формуле (29.1), при полном отсутствии ин­формации о зависимости отказов элементов— по формуле (29.3) при r = 0,5. Показатели надежности конструкции из последователь­но соединенных элементов при независимых отказах всегда меньше показателей надежности каждого из элементов вместе взятых.

Средний срок службы такой системы при экспоненциальном законе распределения отказов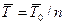

где 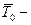средний срок службы одного элемента.

Таким образом, средний срок службы системы при последовательном соединении элементов обратно пропорционален их числу.

Параллельное соединение элементов. Это такое соединение элементов в системе, при котором отказ системы наступает в том случае, если из строя выйдут все элементы. Математические модели систем из параллельно соединенных элементов используют для оценки надежности статически неопределимых систем: неразрезных балок, плит опертых по контуру, колонн одноэтажных зданий, воспринимающих ветровые, сейсмические и другие горизонтальные нагрузки, сплошных вертикальных диафрагм многоэтажных зданий. К системам с параллельным соединением элементов относятся некоторые статически неопределимые фермы. Например, ферма, показанная на рис.29.2 а, может быть представлена в виде параллельного соединения двух элементов (рис. 29.2, б и в).

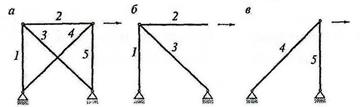
Рис. 29.2. Параллельное соединение элементов статически неопределимой фермы:

а – схема фермы; б, в – структурные элементы фермы; 1,2,3,4,5 – номера стержней фермы.

При анализе статически неопределимых систем следует иметь в виду, что при выходе из строя одной связи наблюдается перераспределение усилий, перезагрузка неотказавших элементов, а условие независимости отказов нарушается.

В случае, параллельного соединения элементов с независимыми отказами вероятность отказа определяется как произведение отказов элементов, а надежность системы

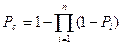(29.5)

При параллельном соединении элементов с независимыми отказами надежность системы выше надежности любого отдельного элемента. Так, если число элементов n = 2, а надежность работы каждого элемента P₁ = P₂ = 0,95, то надежность системы P_с= 0,9975.

В том случае, когда отказы элементов полностью зависимы, вероятность безопасной работы системы равна вероятности безотказного функционирования наиболее надежного элемента P_i,max:

Р_с = Р_i,max (29.6)

В общем случае двусторонние оценки надежности системы с параллельным соединением будут:

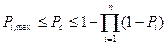(29.7)

Согласно (29.7) статически неопределимые конструкции как системы с параллельным соединением элементов обладают более высокой надежностью, чем статически определимые конструкции. Следовательно, элементы статически неопределимых систем могут иметь более низкие значения вероятностных показателей, чем элементы статически определимых конструкций.

При линейной зависимости между вероятностями безотказной работы элементов системы надежность конструкции с параллельными соединениями элементов

Р_с = Р_нез – r(Р_нез – Р_i,min), (29.8)

или

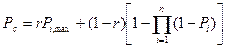(29.9)

где 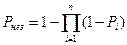— вероятность безотказной работы при независимых отказах;

r— обобщенный коэффициент корреляции.

Средний срок службы системы с параллельным соединением элементов при независимых отказах и экспоненциальном законе распределения надежности каждого элемента

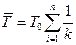(29.10)

где-T₀ — средний срок службы одного элемента (k = 1).

Срок службы системы с параллельным соединением элементов увеличивается с ростом их числа. Пусть n = 3, тогда средний срок службы согласно (29.10) равен:

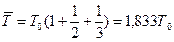
Практически в сложных системах под воздействием нагрузок элементы взаимодействуют между собой одновременно при последовательном и параллельном соединении. Такое взаимодействие, например, наблюдается для круглого или овального в плане вантового покрытия, состоящего из большего числа (n = 100) радиально расположенных вант. Ванты прикреплены к наружным и внутренним распорным кольцам. Если произойдет отказ одного или нескольких вант на разных участках покрытия, то это не обязательно приведет к аварии. При отказе нескольких соседних вант нагрузка на элементы, ограничивающие поврежденный участок, может превысить разрушающую, и тогда выход из строя всей системы неизбежен. Конструкция вантового покрытия, запроектированная с учетом взаимодействия с точки зрения надежности составляющих ее элементов, способных до некоторой степени дублировать другие, обладает дополнительной надежностью и устойчивостью к отказам по отношению к отдельным элементам и узлам соединений.

Пример 29.3.Горизонтальные нагрузки в многоэтажных зданиях рамносвязевой системы воспринимаются вертикальными диафрагмами жесткости и поперечными рамами (рис. 29.3). Диафрагмы и рамы объединены в горизонтальной плоскости перекрытиями и образуют систему с параллельным соединением элементов. Требуется оценить безопасность конструкции, воспринимающей ветровую нагрузку, при следующих вероятностях безотказной работы элементов системы и при коэффициенте корреляции

r = 0,61:

P_i = 0,99 для торцевой диафрагмы 1 (см. рис. 29.3)

Р₂= 0,962 для поперечных рам;

Р₃= 0,994 для торцевой диафрагмы 3

Вероятность безопасной работы системы определяем при n = 3 по формуле (29.9)

P_c = 0,61∙0,994+(1-0,61)[1-(1~0,99)∙(1-0,962)∙(1-0,994)] = 0,9963.

Надежность системы из трех элементов выше надежности наиболее надежного звена (0,9963 > 0,994).

Смешанное соединение элементов представляет собой комбинацию последовательного и параллельного соединений элементов. Модели смешанных соединений элементов могут быть использованы при проектировании следующих конструкций: монолитные балочные перекрытия; рамы и безраскосные фермы; вертикальные диафрагмы жесткости многоэтажных зданий с вертикальными рядами проемов и др.

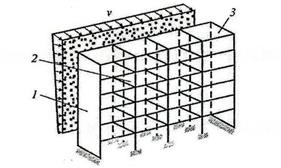
Рис. 29.3. К оценке безопасной работы конструкции рамно-связевой системы:

1,3 – торцевые диафрагмы; 2 – поперечные рамы.

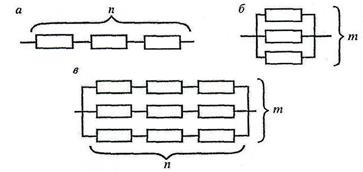
Рис. 29.4. Блок-схема соединений элементов в системе:

а — последовательное соединение; б—параллельное соединение;

в — смешанное соединение.

Расчет надежности систем со смешанным соединением зависит от конкретной схемы соединения. При смешанном соединении, показанном на рис. 29.4, в, n элементов соединены между собой последовательно, a m — параллельно. Надежность такого соединения можно определить, вычисляя сначала вероятность безопасной работы каждой цепи последовательно соединенных элементов по формуле (29.3), а затем, рассматривая каждую цепь как самостоятельный элёмент и переходя к вероятности неразрушения системы параллельно соединенных m элементов, получим выражение для определения надежности такой системы

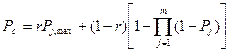(29.11)

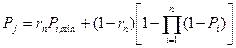(29.12)

где P_j - вероятность работоспособности j-й подсистемы, состоящей из и последовательно соединенных элементов; .

r_п— обобщенный показатель корреляции подсистемы.