Основные методы вероятностного расчета строительных конструкций
При проектировании строительных конструкций представляется весьма важным установить соответствие расчетной модели действительной работе конструкций в эксплуатации и правильно учитывать изменчивость случайных факторов. Расчет начинается с анализа структурной схемы сооружения и распределений несущей способности и внешних воздействий. Отсутствие отказов характеризуется тем, что усилия от нагрузок F не превышают несущую способность Ф, т. е.
| (26.1) |
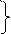 Ф-F>0
Ф-F>0
Ф/F>1
В силу случайной природы прочности и нагрузок условие (26.1) не может быть выполнено абсолютно точно; оно соблюдается с некоторой вероятностью, достаточно близкой к единице, в течение срока службы сооружения. По мере развития теории надежности предлагались различные методы расчета надежности строительных конструкций.
Метод Н. С. Стрелецкого
Им впервые исследовались совместно вероятностные распределения нагрузки и несущей способности.
Пусть кривая распределения прочности характеризуется математическим ожиданием  и среднеквадратичным отклонением
и среднеквадратичным отклонением  -, а кривая распределения усилия от нагрузки — соответственное и F. Эти кривые пересекаются в одной точке, соответствующей несущей способности Фо и усилию от нагрузки — Fo (рис. 26.1). Значения Фо = Fqзависят от общего коэффициента запаса и могут быть приняты за расчетные. Для оценки безопасной работы конструкции Н. С. Стрелецкий ввел понятие «гарантия неразрушимости» и дал простой способ ее определения:
-, а кривая распределения усилия от нагрузки — соответственное и F. Эти кривые пересекаются в одной точке, соответствующей несущей способности Фо и усилию от нагрузки — Fo (рис. 26.1). Значения Фо = Fqзависят от общего коэффициента запаса и могут быть приняты за расчетные. Для оценки безопасной работы конструкции Н. С. Стрелецкий ввел понятие «гарантия неразрушимости» и дал простой способ ее определения:
 (26.2)
(26.2)
где Г— гарантия неразрушимости (вероятность безотказной работы);
 — вероятность того, что прочность конструкции получит заниженные зна чения Ф < Ф0;
— вероятность того, что прочность конструкции получит заниженные зна чения Ф < Ф0;
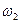 — вероятность того, что нагрузка получит завышенное значение, т. е. F > F0;
— вероятность того, что нагрузка получит завышенное значение, т. е. F > F0;
 — вероятность одновременного появления этих событий (вероятность отказа).
— вероятность одновременного появления этих событий (вероятность отказа).
В такой трактовке отказ происходит при одновременном появлении двух событий: снижения несущей способности ниже расчетной и превышения нагрузками расчетной величины.
Вероятности  и
и 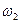 нетрудно вычислить, если известны законы распределения нагрузки и несущей способности. Они равны площадям криволинейных треугольников, заключенных между осью абсцисс и отрезками кривых в диапазоне от Фо до
нетрудно вычислить, если известны законы распределения нагрузки и несущей способности. Они равны площадям криволинейных треугольников, заключенных между осью абсцисс и отрезками кривых в диапазоне от Фо до 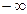 для распределения несущей способности и от F0 до +
для распределения несущей способности и от F0 до + 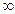 для распределения нагрузок:
для распределения нагрузок:

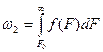 . (26.3)
. (26.3)
На практике для вычисления  и
и 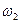 используются таблицы интеграла вероятностей.
используются таблицы интеграла вероятностей.
Однако гарантия неразрушимости служит примерной и завышенной оценкой вероятности безотказной работы, так как не учитывает все возможные сочетания нагрузок и несущей способности. Впоследствии была дана двусторонняя оценка для вероятности отказа Q=1-Г:
 , (26.4)
, (26.4)
если обе кривые распределения имеют по одному максимуму.
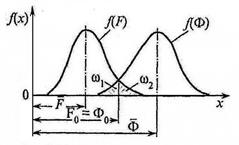
Рис. 26.1. К определению «гарантии неразрушимости»
Пример 26.1. Оценить вероятность отказа изгибаемой балки при следующих исходных данных:  = 280 кНм,
= 280 кНм,  = 20 кНм ,
= 20 кНм ,
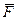 =180 кНм, F = 20 кНм. Пересечение двух распределений находится в точке Ф. = F() = 240 кНм; распределения Ф и F нормальные.
=180 кНм, F = 20 кНм. Пересечение двух распределений находится в точке Ф. = F() = 240 кНм; распределения Ф и F нормальные.
Вычисляем вероятности  и
и  , используя функции Лапласа:
, используя функции Лапласа:
 ;
; 
Зная uФ и uF по таблицам интеграла вероятностей находим, что 
 .
.
Двусторонние оценки вероятности отказа
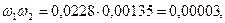
 .
.
Итак, 0,00003<Q<0,02412
Двусторонние оценки для гарантии неразрушимости следующие: 0,97588<Г<0,99997.
Метод А. Р. Ржаницына
Рассмотрим вначале случай, когда усилие от нагрузки описывается случайной величиной с плотностью распределения fF(F), а прочность принимает одно детерминированное значение Фдет (рис. 26.2).

Рис. 26.2. Плотности распределения несущей способности fФ(Ф) (кривая 1) и нагрузок fF(F) (кривая 2).
Тогда отказ наступит в том случае, когда усилие от нагрузки превысит значение прочности Фдет, F-Фдет > 0 с вероятностью Q, равной заштрихованной площади  :
:
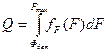 ,
,
где F – максимальное значение нагрузки.
Тогда вероятность безопасной работы (надежность)
Р = 1 – Q (26.5)
Если нагрузка и прочность – случайные величины, то для нахождения вероятности отказа вводится случайная величина, которая называется резервом прочности и равна
 (26.6)
(26.6)
Отказ происходит, когда
Ф – F < 0 или 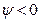 . (26.7)
. (26.7)
Область отказа определяется отрицательными значениями  , а вероятность отказа равна заштрихованной площади на рис 26.3. и определяется так:
, а вероятность отказа равна заштрихованной площади на рис 26.3. и определяется так:
 (26.8)
(26.8)
где 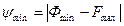 .
.
Вероятность безотказной работы по-прежнему определяется формулой (26.5). Следовательно, для определения вероятности безотказной работы конструкции необходимо знать распределение резерва прочности. На основе теории вероятностей закон распределения разности случайных величин имеет вид:
 (26.9)
(26.9)
где Фmin и Фmax – минимальное и максимальное значения несущей способности.
Формула (26.9) справедлива, если нагрузка и прочность статистически независимы.
Приведенные формулы значительно упрощаются при нормальных законах распределения. Пусть
 и
и 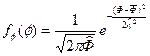
где 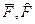 и
и  — математическое ожидание и стандарт распределения усилий соответственно от нагрузки и несущей способности.
— математическое ожидание и стандарт распределения усилий соответственно от нагрузки и несущей способности.
Распределение разности случайных величин, распределенных по нормальному закону, будет также нормальным:
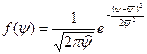
с параметрами 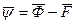 и
и  .
.
Вероятность отказа
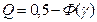 (26.10)
(26.10)
где 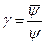 - число стандартов, укладывающихся в интервале от
- число стандартов, укладывающихся в интервале от 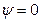 до
до 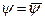 ;
;
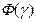 - интеграл вероятностей:
- интеграл вероятностей: 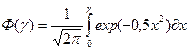
Для интеграла вероятностей составлены таблицы, которые приводятся в справочниках и книгах по теории вероятностей. Величину 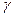 называют характеристикой безопасности.Определенному значению
называют характеристикой безопасности.Определенному значению 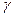 соответствует вероятность отказа (например,
соответствует вероятность отказа (например, 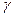 = 1,28 соответствует Q- 0,1). Использование приведенных формул для
= 1,28 соответствует Q- 0,1). Использование приведенных формул для  при нормальных законах распределения нагрузки и несущей способности приводит к следующей расчетной формуле:
при нормальных законах распределения нагрузки и несущей способности приводит к следующей расчетной формуле:
 (26.11)
(26.11)
где 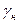 характеристика безопасности, соответствующая нормативному значению надежности; при Рн= 0,9987 величина
характеристика безопасности, соответствующая нормативному значению надежности; при Рн= 0,9987 величина 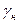 = 3.
= 3.
Для применения формул (26.3—26.9) необходимо знать плотности распределения нагрузки, несущей способности и решение соответствующей детерминистической задачи для всей интересующей нас области изменения случайных параметров. Решение этих задач дается методами строительной механики с учетом особенностей применяемых материалов. Таким образом, вероятностный подход предполагает решение детерминистической задачи, расширяет ее возможности, дает оценку точности решения и определяет количественную меру риска выхода из строя конструкций.

Рис. 26.3. Плотность распределения резерва прочности:
1 - область безотказной работы; 2 – область отказов.
Пример 26.2. Определить надежность железобетонного ригеля перекрытия.
Исходные данные:
математическое ожидание несущей способности ригеля
 = 220 кН∙м;
= 220 кН∙м;
коэффициент вариации распределения несущей способности
VФ= 0,1;
математическое ожидание изгибающего момента от нагрузки.
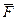 = 130 кНм;
= 130 кНм;
коэффициент вариации распределения изгибающего момента от нагрузки VF = 15;
характеристика безопасности 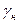 = 3;
= 3;
нормативное значение надежности Рн=0,9987
Стандарты распределений:
для несущей способности  = 0,1∙220 = 22 кН∙м;
= 0,1∙220 = 22 кН∙м;
для изгибающего момента от нагрузки F=VF 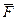 = 0,15∙130 = 19,5 кН∙м.
= 0,15∙130 = 19,5 кН∙м.

 Характеристике безопасности
Характеристике безопасности 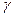 = 3,06 соответствует надежность Р1 = 0,99889, что выше нормативной Рн = 0,9987. Надежность работы ригеля при действии нагрузок считается обеспеченной.
= 3,06 соответствует надежность Р1 = 0,99889, что выше нормативной Рн = 0,9987. Надежность работы ригеля при действии нагрузок считается обеспеченной.
Пример 26.3. При изготовлении железобетонных ригелей перекрытий приняты меры по повышению качества изделия. Бетон стал более однородным, а коэффициент вариации несущей способности снизился до значения VФ’ = 0,07. Определить надежность работы ригеля и наметить пути снижения расхода конструктивных материалов. Данные для расчета принимаются такими же, как в примере 26.2, кроме значения Vф.
Стандарт распределения несущей способности
 кНм.
кНм.
Характеристику безопасности можно определить по формуле (26.11):
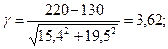
Характеристике безопасности 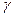 = 3,62 соответствует надежность Р2 = = 0,99885,
= 3,62 соответствует надежность Р2 = = 0,99885,
Определим вероятность отказа для условий примеров 26.2 и 26.3:
при Vф = 0,1 (пример 6.3) Q1 = 1 – P1 = 1 – 0,99889 = 0,00111;
при Vф, = 0,1 (пример 6.3) Q2 = 1 – P2 = 1 – 0,99885 = 0,00115;
Вероятность отказа в примере 26.3 уменьшилась в  раза после принятия технологических мер по повышению качества конструкции, что повысило ее надежность, которая превышает нормативное значение. В результате улучшения технологии изготовления создались условия для уменьшения расхода материалов при сохранении нормативной надежности. С этой целью найдем значение средней несущей
раза после принятия технологических мер по повышению качества конструкции, что повысило ее надежность, которая превышает нормативное значение. В результате улучшения технологии изготовления создались условия для уменьшения расхода материалов при сохранении нормативной надежности. С этой целью найдем значение средней несущей  с заданной нормативной надежностью:
с заданной нормативной надежностью:
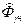 =F+
=F+ 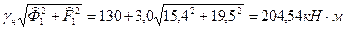
При несущей способности  =204,54 кН∙м обеспечивается нормативная надежность, а расход материалов может быть снижен примерно на
=204,54 кН∙м обеспечивается нормативная надежность, а расход материалов может быть снижен примерно на 
Нормативное значение вероятности безотказной работы строительной конструкции представляет собой величину, близкую к единице. Она устанавливается исходя из требований обеспечения безопасной работы технологического оборудования и людей, безопасности движения для транспортных сооружений и минимума общих затрат на строительные и эксплуатационные работы. Следует отметить, что эти требования экономически противоречивы.
Повышение надежности ведет к увеличению запасов несущей способности конструкции, которые не всегда могут реализовываться в течение срока эксплуатации и вызывают неоправданное удорожание. В то же время конструкции с уменьшенными размерами поперечных сечений несущих элементов и расходом материалов обладают сниженной надежностью.
Отказы конструкций приводят к различного рода ущербам. К ним относятся стоимость С1 восстановления отучавшей конструкции и ее ремонта при эксплуатации, затраты С2 на восстановление оборудования и других частей поврежденных сооружений, потери С3 прибыли производства на время его остановки вследствие отказа. Значение нормативной надежности конструкции с экономической ответственностью, размер ущерба для которых может быть оценен в стоимостном выражении, устанавливается из условия минимума общих затрат на строительные и текущие работы при эксплуатации зданий и сооружений (рис. 26.4):
С=С0(Р)+Сэ(Р)→min, (26.12)
где С—общая стоимость;
С0(Р) — начальная строительная стоимость конструкции;
Сэ(Р) — затраты в процессе эксплуатации, связанные с отказами конструкции и ее содержанием: Сэ(Р) = С1+ С2 + С3
Оба слагаемых формулы (26.12) зависят от надежности Р: с увеличением Р возрастает C0(P) , но снижаются эксплуатационные расходы Сэ(Р) (см. рис. 26.4).

Рис. 26.4. Зависимость общей стоимости конструкции С от ее надежности Р.
Затраты Cэ(Р) должны учитывать отдельные эксплуатационные расходы во времени на основе приведения разновременных затрат к единому показателю. Если не ограничивать значения Р, то в результате получается оптимизация и реализуется некоторый компромисс между требованиями надежности и экономичности. Однако необходимо обеспечить безопасность людей. Кроме того, следует также учитывать повреждения исторических и культурных памятников, другие виды ущерба, не имеющие стоимостного выражения, такие, как нарушение нормальной работы учреждений, бытовые неудобства, невыполнение эстетических требований. Поэтому нормативное значение надежности должно быть ограничено некоторыми минимальными значениями с учетом ответственности, архитектурных достоинств и других особенностей зданий и сооружений:
Рн ≥ P*,
где P* - минимально допустимое нормативное значение надежности.
Вопрос о нормативной надежности пока не нашел окончательного решения, особенно для объектов с неэкономической ответственностью, когда ущерб от наступления отказов не оценивается явно в стоимостной форме.
Для корректного решения задачи можно воспользоваться несколькими подходами.
Первый заключается в том, что значение нормативной надежности находят минимизацией функционала полной стоимости проектируемой системы, куда входит стоимость: материала, изготовления, транспортировки, эксплуатационных расходов, приведенных капитальных затрат, ущерба от возможного отказа и потерянной прибыли и вследствие возможных аварий за время эксплуатации системы.
Второй подход предусматривает анализ надежности эксплуатируемых конструкций и элементов зданий и сооружений, а также информации о потоках их отказов.
Третий подход состоит в анализе той надежности, которая заложена в конструкциях, запроектированных по нормам своего времени. При этом следует иметь в виду, что при составлении норм авторы не ставили задачу расчета надежности строительных конструкций.
Поскольку конструкции, запроектированные по нормам, имеют излишние запасы прочности, возможен следующий способ назначения нормативного значения надежности. Он заключается в том, что на основе оценки общего числа N функционирующих элементов рассматриваемого типа в зданиях и сооружениях
(с учетом перспективы) вводится величина Р =1-1/Nкоторая и служит искомой надежностью.
Объективные значения нормативных показателей надежности должны определяться для каждого отдельного вида строительных конструкций на основе глубоких теоретических разработок и обширных экспериментальных исследований.
В нашей стране на основе многолетней эксплуатации различных инженерных систем в зависимости от ответственности элемента, конструкции, объекта получены следующие данные нормативных значений надежности (табл. 26.1).
Таблица 26.1
Ориентировочные значения нормативной надежности
| Элемент конструкции или сооружения | Начало эксплуатации | Окончание эксплуатации |
| Малоответственный элемент конструкции | 0,90...0,95 | 0,85...0,90 |
| Массовый элемент статистически неопределимой конструкции, отказ которой не влечет внезапного разрушения системы | 0,99 | 0,95 |
| Ответственная конструкция (ферма, балка, колонна) с постепенными отказами | 0,999 | 0,99 |
| Ответственная конструкция с внезапными отказами | 0,9999 | 0,999 |
| Уникальное сооружение | 0,99999 | 0,9999 |
Значения гауссовского коэффициента надежности железобетонных конструкций, запроектированных по отечественным нормам, равны 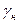 = 3...4. Надежность, соответствующая определенным значениям
= 3...4. Надежность, соответствующая определенным значениям 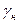 следующая:
следующая:
Надежность 0,9 0,99 0,999 0,9999
Значения 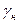 1,28 2,33 3,10 3,76
1,28 2,33 3,10 3,76
Расчеты надежности и долговечности автодорожных мостов свидетельствуют, что оптимальная надежность зависит от срока службы и Рн = 0,99...0,999.
Оптимальное значение надежности составляет: по образованию трещины в защитном слое Рн = 0,90...0,95; по достижении трещинами нормативной ширины раскрытия а = 0,2mm, Рн= 0,95.
В Венгрии согласно нормам MSZ 15020-71 емкостные сооружения надежны при 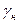 > 3,72. В Чехии и Словакии обеспеченность работоспособности железобетонных элементов соответствует
> 3,72. В Чехии и Словакии обеспеченность работоспособности железобетонных элементов соответствует 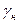 = 2,8...4,0. В ФРГ по результатам исследований профессора Рюша для железобетонных конструкций предлагается принимать следующие вероятности отказов:
= 2,8...4,0. В ФРГ по результатам исследований профессора Рюша для железобетонных конструкций предлагается принимать следующие вероятности отказов:
при отказе без предварительных сигналов (хрупкие разрушения, потеря устойчивости, разрушение оснований);
Q = 10-5…10-7 (что соответствует Рн = 0,99999…0,999999)
Q = 10-4 (т. е. Рн= 0,9999) при достижении предельной несущей способности с предварительными сигналами (текучесть растянутой арматуры при изгибе и др.);
Q = 10-2…10-3 (т.е. Рн = 0,99…0,999) При наступлении состояния непригодности к эксплуатации без потери несущей способности.
В США практика проектирования и строительства сооружений показывает, что в случае применения нормального закона сопротивлений и усилий гауссовский коэффициент надежности железобетонных элементов равен:
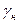 = 2,8...3,2 для опасных нормальных сечений изгибаемых элементов с ненапрягаемой арматурой;
= 2,8...3,2 для опасных нормальных сечений изгибаемых элементов с ненапрягаемой арматурой;
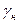 = 3,5...4,0 — то же с напрягаемой арматурой;
= 3,5...4,0 — то же с напрягаемой арматурой;
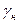 = 3,0...3,5 для опасных нормальных сечений внецентренно сжатых элементов;
= 3,0...3,5 для опасных нормальных сечений внецентренно сжатых элементов;
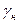 = 2,25...2,40 для опасных наклонных сечений.
= 2,25...2,40 для опасных наклонных сечений.
Обобщенные результаты вероятностной оценки безопасности и эксплуатационной пригодности изгибаемых железобетонных элементов свидетельствуют, что вероятность разрушения конструкции по нормальным сечениям в среднем Q =10-4 u Q = 10-5 соответственно для обычных и предварительно напряженных элементов. Вероятность эксплуатационной пригодности элементов ниже надежности конструкции по исчерпанию несущей способности.
При назначении нормативной надежности должен учитываться опыт проектирования и эксплуатации зданий и сооружений.
Метод В. В. Болотина
Строгий подход к расчету надежности строительных конструкций основан на учете фактора времени . Изменение нагрузок и несущей способности происходят с течением времени, а наступление опасного состояния возникает в результате постепенного накопления повреждений. Например, прочностные и деформативные свойства железобетонной конструкции таковы, что в течение периода эксплуатации в бетоне и арматуре развиваются процессы, изменяющие способность конструкции сопротивляться воздействиям нагрузок и влиянию окружающей среды. Колебания влажности, перепады температур с переходом через ноль, ползучесть бетона вызывают постепенное нарушение его структуры, что ухудшает эксплуатационные качества конструкции. Многократно повторное воздействие нагрузки приводит к развитию усталостных повреждений в металле и бетоне. Процессы коррозии стальных конструкций и арматуры в железобетоне снижают несущую способность. В то же время в начальной стадии нагружения происходит упрочнение бетона, и, следовательно, несущая способность железобетонной конструкции в начальный период эксплуатации может повышаться.
В основу метода В.В. Болотина положено предположение, что поведение конструкций описывается случайным процессом, а отказ рассматривается как случайный выброс характеристик напряженного состояния конструкции из области допустимых состояний.
Общая схема расчета надежности с учетом физических, технических и эксплуатационных аспектов состоит из четырех этапов.
На первом этапе устанавливается расчетная схема системы (сооружения) и внешние случайные воздействия на нее.
На втором этапе определяется стохастическое поведение системы при случайных воздействиях.
Третий этап заключается в выборе пространства и области допустимых состояний. За параметры качества могут приниматься значения напряжений, моментов, нормальных сил, перемещений моментов и другие факторы, характеризующие напряженное состояние конструкции. Область допустимых значений параметров устанавливается на основе технико-экономических соображений с учетом технологических и эксплуатационных требований.
На четвертом этапе рассчитывается функция надежности как дополнение до единицы вероятности случайного выброса за пределы допустимой области.
Область допустимых значений, особенно для железобетонных конструкций, носит случайный характер. Для расчета надежности конструкций, стохастические свойства которых описываются конечным числом параметров, применяется метод условных функций надежности. Сначала рассчитывается надежность внутренне детерминированной системы под действием внешних нагрузок, трактуемых как случайный процесс. Эта надежность называется условной надежностью.Она зависит от случайных параметров, характеризующих свойства системы, — механические свойства материалов, начальные дефекты, возможные отступления геометрических размеров от номинальных. Совместная плотность вероятностей f(x1,x2,…xn) этих параметров должна быть получена путем изучения и обобщения представительной статистической информации. Затем применяется формула полной вероятности для данной системы:
 (26.13)
(26.13)
Здесь Q(F>Ф/x1,x2,…,xn;t) - условная вероятность того, что нагрузка F превышает несущую способность Ф при фиксированных значениях параметров прочности x1,x2,…,xn за период времени t.
В частности, при нагрузках, описываемых стационарным гауссовским процессом, формула для определения надежности ансамбля конструкций приобретает вид:
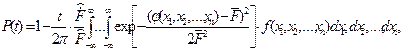 (26.14)
(26.14)
где  - функциональная зависимость несущей способности от случайных параметров x1,x2,…,xn;
- функциональная зависимость несущей способности от случайных параметров x1,x2,…,xn;
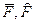 — математическое ожидание и стандарт процесса нагружения;
— математическое ожидание и стандарт процесса нагружения;
 — стандарт скорости изменения процесса нагружения.
— стандарт скорости изменения процесса нагружения.
При наличии обширной исходной статистической информации и выборе критериев отказа задача определения надежности сводится к решению кратных интегралов (26.13), (26.14). Стремление к аналитическому выражению функции надежности связано с рядом допущений.
Дата добавления: 2015-02-16; просмотров: 5374;
