Теплота

Под теплотой понимают количество энергии, которой термо­динамическая система обменивается с окружающей средой микроскопическим путем (теплообменом).

Обмен энергией в форме теплоты возможен и между телами внутри системы.

Теплота здесь понимается только как форма передачи энергии, и неверно говорить, что она выражает свойство системы, тем более содержится в системе. Можно говорить о теплоте, подведенной к системе или от нее отведенной, но нельзя говорить об увеличении или уменьшении теплоты в той или иной системе, т.е. не следует путать теплоту и внутреннюю тепловую энергию.

Теплоту обозначают Q. За единицу теплоты принят джоуль. В термодинамике подводимую теплоту принято считать положительной, отводимую – отрицательной.

Вторая форма передачи энергии связана с изменением объема системы и перемещением ее в окружающей среде под воздействием различных силовых полей – гравитационного, упругостного, магнитного; поля сил давления и др. Такая форма энергообмена, реализуемая макроскопическим путем, называется р а б о т о й.

Работа

Под работой понимают количество энергии, которой термодинамическая система обменивается с окружающей средой в результате макроскопического, упорядоченного, направленного движения.

Работа обозначается L. За единицу работы принят джоуль.

В термодинамике работу, совершаемую системой по преодолению внешних сил, принято считать положительной, а совершаемую внешними силами над системой - отрицательной. Работа, связанная с увеличением объема системы, называется работой расширения (L_расш.); с уменьшением объема – работой сжатия (L_сж.).

Работа процесса

В общем случае термодинамическая система может совершать одновременно работу по увеличению своего объема; работу по преодолению внешних сил давления, сил трения; работу по преодолению воздействия гравитационных, магнитных и других полей. Тогда техническая (полезная) работа системы с учетом правила знаков может быть выражена в виде:

L_тех = L_расш - L_д - ∑L_пр , (1.8)

где L_тех – техническая работа системы;

L_расш – работа расширения;

L_д – работа по преодолению поля сил давления;

∑L_пр – сумма работ по преодолению сил трения, гравитационных,

магнитных и прочих полей.

Выразим работу через термодинамические параметры. Пусть система

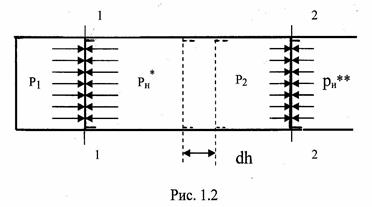
dL_{расш =} pF dh,

где F – площадь поршня;

p – давление газа, имеющее величину p₁> p> p₂.

Так как Fdh = dV, то dL _расш = pdV.

Проинтегрировав последнее выражение от начального состояния до конечного, получим:

L_расш = 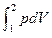. (1.9)

При увеличении объема системы не вся работа расширения полезно использована, часть ее затрачена на вытеснение среды. Для того, чтобы ввести систему объемом V в окружающую среду с давлением p, необходимо затратить работу по преодолению поля сил давления среды, равную pV. Для рассматриваемого примера эта работа будет равна:

L_д = p_н^**V₂ – p_н^*V.

Так как при равновесном процессе p_н^* = р₁ и р_н^**= р₂, то

L_д= p₂V₂ – p₁V₁ = . (1.10)

Для систем, расматриваемых в технической термодинамике, величиной ∑L_пр в (1.8) можно пренебречь, тогда техническая работа будет равна разности между работой расширения и работой по преодолению поля сил давления:

L_тех = L_расш – L_д.

Используя выражения (1.9) и (1.10), получим:

L_тех = – 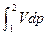. (1.11)

Обратимся к выражению (1.8). Если сумма работ по определению сил трения, гравитационных, магнитных и прочих полей принять равной нулю, то работа системы при переходе из одного состояния в другое есть не что иное, как работа техническая.

Правые части выражений (1.9) и (1.11) представляют собой определенные интегралы непрерывных и положительных внутри промежутка 1-2 функций. Такие интегралы имеют простое геометрическое истолкование. Так, интеграл вида 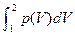численно равен площади под кривой функции p(V), изображенной на графике, рис. 1.3, где по оси ординат отложено давление, а по оси абсцисс – объем. Интеграл – 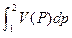= 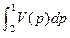также численно равен площади под кривой, но уже функции V(p), изображенной в координатах pV, рис.1.4. Отсюда работа расширения численно равна площади, ограниченной кривой процесса 1-2, ординатами V₁ и V₂ и осью абсцисс, т.е. L_расш = F_1-2-V2-V1-1.

Техническая работа численно равна площади, ограниченной кривой процесса 1-2, абсциссами p₁ и p₂ и осью ординат, т.е. L_тех =L _2-P2-P1-1.

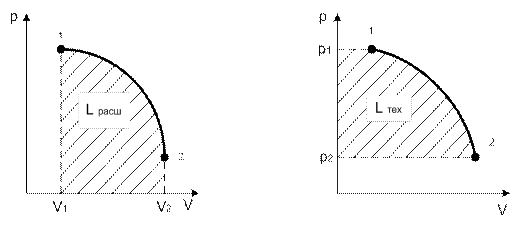
Рис. 1.3 Рис. 1.4.

Работа процесса зависит не только от параметров начального и конечного состояний, но и от того, по какому пути осуществляется этот процесс. Как видно из рис.1.5, работа расширения и работа техническая будут существенно различаться в процессах 1-а-2, 1-б-2 и 1-с-2.

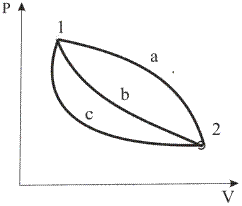Отсюда работа как термодинамическая величина есть, прежде всего ф у н к ц и я п р о ц е с с а. Теплоту и работу, отнесенные к массе системы, называют п р и в е д е н н ы м и или удельными Приведенная теплота q и приведенная работа l выражаются в Дж/кг и .вычисляются с помощью соотношений.

q = Q / m и l = L / m.

Учитывая это, выражения (1.9) и (1.11) за пишутся:

Рис. 1.5 l_расш = 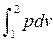и l_тех = – . .

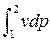Здесь рассматриваются системы, в которых протекают о б р а т и м ы е процессы, хотя в действительности все реальные процессы в той или иной степени н е о б р а т и м ы.

Обратимым называют такой процесс, который может быть осуществ- лен в обратном направлении через те же состояния и точно с тем же обменом энергии в форме теплоты и работы, что и в прямом напправлении.

Это значит, что Q_{п р}= Q_обр и L_{п р}= L_обр. Если хотя бы одно из условий не выполняется, то процесс необратим. Типичным примером нарушения условия обратимости является протекание процесса при наличии трения, так как результатом трения является необратимое преобразование работы в теплоту.