Скрытая теплота испарения
При испарении жидкости из нее переходят в пар наиболее быстрые молекулы, обладающие большей средней кинетической энергией, чем молекулы, остающиеся в жидкости. Отсюда следует, что если испаряющаяся жидкость теплоизолирована, то ее температура будет понижаться. Чтобы температура испаряющейся жидкости не понижалась, к ней необходимо подводить тепло.
Количество тепла, которое необходимо для того, чтобы испарить определенную массу жидкости без изменения ее температуры при внешнем давлении, равном давлению насыщенныхпаров, называетсяскрытой теплотой испарения.Скрытая теплота испарения единицы массы жидкости называется удельной скрытой теплотой испарения.Скрытая теплота испарения одного моля жидкости называется молярной скрытой теплотой испарения.
Скрытая теплота испарения определяется силами связи между молекулами жидкости. Чем эти силы больше, тем больше скрытая теплота испарения.
«Скрытость» скрытой теплоты испарения заключается в том, что она не идет на нагревание жидкости, а идет на совершение работы по отрыву от жидкости молекул, переходящих в пар.
Скрытая теплота испарения в общем случае зависит от температуры, при которой испарение происходит. При критической температуре, когда исчезает различие между жидкостью и ее насыщенным паром, скрытая теплота испарения равна нулю.
Конденсация некоторой массы пара сопровождается выделением такого же количества тепла, которое необходимо для испарения этой массы жидкости. Поэтому скрытую теплоту испарения называют также скрытой теплотой конденсации или скрытой теплотой перехода.
Итак, при фазовом переходе «жидкость-пар», происходящем без изменения температуры системы, внутренняя энергия системы изменяется в результате подвода к системе или отвода от нее скрытой молярной теплоты испарения: внутренняя энергия пара больше, чем внутренняя энергия жидкости той же массы при той же температуре.
Пример 13.3. Скрытая молярная теплота 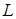 испарения воды при температуре
испарения воды при температуре 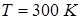 равна
равна 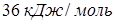 . Вычислим, какая часть скрытой теплоты испарения, подводимой к системе «вода-пар», идет на увеличение ее внутренней энергии, если температура системы при испарении не меняется.
. Вычислим, какая часть скрытой теплоты испарения, подводимой к системе «вода-пар», идет на увеличение ее внутренней энергии, если температура системы при испарении не меняется.
Пусть квазистатически испарился один моль воды, превратившись в насыщенный пар, имеющий температуру 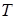 и давление
и давление 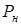 . Применяя к образовавшемуся пару уравнение состояния идеального газа, имеем:
. Применяя к образовавшемуся пару уравнение состояния идеального газа, имеем:
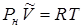 ,
,
где 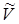 - объем моля насыщенного пара. Поскольку этот объем велик по сравнению с объемом одного моля воды, то приращение объема системы «жидкость - пар» в результате испарения моля жидкости можно считать равным
- объем моля насыщенного пара. Поскольку этот объем велик по сравнению с объемом одного моля воды, то приращение объема системы «жидкость - пар» в результате испарения моля жидкости можно считать равным 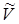 . Так как испарение происходило при постоянном давлении
. Так как испарение происходило при постоянном давлении 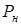 , то совершенная системой работа
, то совершенная системой работа 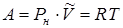 . Количество тепла, подведенного при этом процессе к системе, равно
. Количество тепла, подведенного при этом процессе к системе, равно 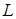 . Применяя первое начало термодинамики, получим:
. Применяя первое начало термодинамики, получим:
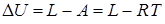 ,
,
где 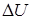 - приращение внутренней энергии системы. Получим:
- приращение внутренней энергии системы. Получим:
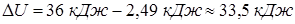 .
.
Таким образом, почти вся подводимая к воде скрытая теплота испарения идет на увеличение внутренней энергии системы и лишь мала ее доля идет на совершение системой при ее расширении механической работы.
Задача 13.3. Вода массы 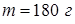 , при температуре
, при температуре 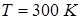 целиком превратилась в насыщенный пар. Найти приращение энтропии этой системы.
целиком превратилась в насыщенный пар. Найти приращение энтропии этой системы. 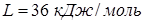 .
.
Ответ: 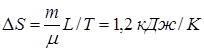 .
.
13.5. Температурная зависимость упругости насыщенных паров над
жидкостью
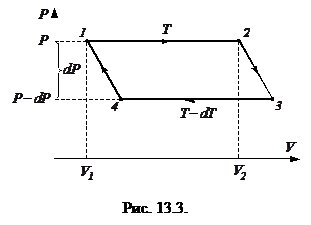 Для нахождения зависимости давления насыщенного пара над жидкостью от температуры рассмотрим цикл Карно, совершаемый двухфазной системой, состоящей из жидкости и ее насыщенного пара, рис. 13.1. В ходе цикла система получает тепло от нагревателя, имеющего температуру
Для нахождения зависимости давления насыщенного пара над жидкостью от температуры рассмотрим цикл Карно, совершаемый двухфазной системой, состоящей из жидкости и ее насыщенного пара, рис. 13.1. В ходе цикла система получает тепло от нагревателя, имеющего температуру 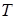 , и отдает тепло холодильнику, имеющему бесконечно близкую температуру
, и отдает тепло холодильнику, имеющему бесконечно близкую температуру 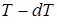
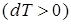 . Цикл состоит из двух адиабатных процессов и двух изотермических. Поскольку адиабатные участки цикла
. Цикл состоит из двух адиабатных процессов и двух изотермических. Поскольку адиабатные участки цикла 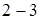 и
и 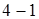 бесконечно малы, то они являются прямолинейными отрезками на графике процесса в координатах
бесконечно малы, то они являются прямолинейными отрезками на графике процесса в координатах 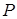 ,
, 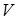 , рис 13.3. Так как при квазистатическом изотермическом процессе давление насыщенного пара не меняется, то изотермы рассматриваемой двухфазной системы являются также ее изобарами (участки
, рис 13.3. Так как при квазистатическом изотермическом процессе давление насыщенного пара не меняется, то изотермы рассматриваемой двухфазной системы являются также ее изобарами (участки 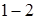 и
и 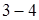 ).
).
Пусть вначале двухфазная система находится в состоянии 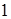 и ее температура равна температуре нагревателя
и ее температура равна температуре нагревателя 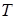 . Приведем систему в тепловой контакт с нагревателем и будем медленно поднимать поршень, рис. 13.1, так, чтобы пар оставался насыщенным, до тех пор, пока не испарится один моль жидкости. Давление насыщенного пара на стадии
. Приведем систему в тепловой контакт с нагревателем и будем медленно поднимать поршень, рис. 13.1, так, чтобы пар оставался насыщенным, до тех пор, пока не испарится один моль жидкости. Давление насыщенного пара на стадии 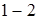 равно
равно 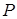 .Система окажется в состоянии
.Система окажется в состоянии 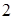 . В соответствии с определением скрытой молярной теплоты испарения
. В соответствии с определением скрытой молярной теплоты испарения 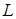 , см подраздел 13.4, система получит на стадии
, см подраздел 13.4, система получит на стадии 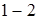 от нагревателя количество тепла
от нагревателя количество тепла
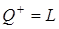 . (13.7)
. (13.7)
В точке 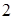 тепловой контакт с нагревателем прерывается и поршень в условиях теплоизоляции системы поднимается еще на бесконечно малое расстояние, так что пар, давящий на поршень, совершает за счет внутренней энергии системы бесконечно малую работу и температура системы уменьшается на
тепловой контакт с нагревателем прерывается и поршень в условиях теплоизоляции системы поднимается еще на бесконечно малое расстояние, так что пар, давящий на поршень, совершает за счет внутренней энергии системы бесконечно малую работу и температура системы уменьшается на 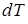 , то есть становится равной температуре холодильника
, то есть становится равной температуре холодильника 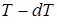 (точка
(точка 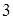 ). Система приводится в тепловой контакт с холодильником и медленным опусканием поршня изотермически сжимается. Давление насыщенного пара на стадии
). Система приводится в тепловой контакт с холодильником и медленным опусканием поршня изотермически сжимается. Давление насыщенного пара на стадии 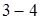 равно
равно 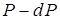 . В точке
. В точке 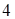 тепловой контакт с холодильником прерывается и дальнейшим бесконечно малым опусканием поршня система адиабатически переводится в исходное состояние
тепловой контакт с холодильником прерывается и дальнейшим бесконечно малым опусканием поршня система адиабатически переводится в исходное состояние 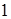 . Положительную работу на стадии
. Положительную работу на стадии 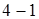 совершает внешняя сила, сжимающая насыщенный пар. Работа этой силы идет на увеличение внутренней энергии системы и сопровождается повышением температуры от значения
совершает внешняя сила, сжимающая насыщенный пар. Работа этой силы идет на увеличение внутренней энергии системы и сопровождается повышением температуры от значения 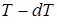 до значения
до значения 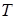 .
.
Работа, совершенная системой в ходе цикла, численно равна площади параллелограмма 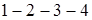 ,
,
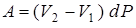 . (13.8)
. (13.8)
где 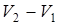 - разность объемов системы в состояниях
- разность объемов системы в состояниях 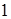 и
и 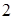 . Эта разность объемов соответствует тому, что один моль жидкости на стадии
. Эта разность объемов соответствует тому, что один моль жидкости на стадии 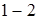 превратился в один моль насыщенного пара,
превратился в один моль насыщенного пара,
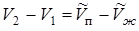 , (13.9)
, (13.9)
где 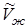 - объем одного моля жидкости,
- объем одного моля жидкости, 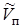 - объем одного моля насыщенного пара.
- объем одного моля насыщенного пара.
Вычислим к.п.д. цикла. Используя (13.7 - 13.9), получим:
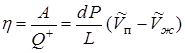 . (13.10)
. (13.10)
С другой стороны, к.п.д. цикла Карно можно выразить через температуры нагревателя и холодильника,
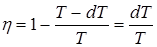 . (13.11)
. (13.11)
Из (13.10), (13.11) получим:
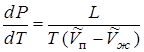 . (13.12)
. (13.12)
Уравнение (13.12) связывает температуру и давление насыщенного пара и называется уравнением Клапейрона-Клаузиуса.
Пусть температура не слишком близка к критической, так что можно положить
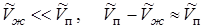 . (13.13)
. (13.13)
Применяя к одному молю насыщенного пара уравнение состояния идеального газа
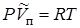 ,
,
получим из (13.12) с учетом (13.13):
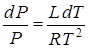 . (13.14)
. (13.14)
Проинтегрируем последнее равенство, считая, что 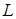 не зависит от температуры. Имеем:
не зависит от температуры. Имеем:
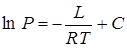 , (13.15)
, (13.15)
где 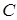 - постоянная интегрирования. Пусть известно давление
- постоянная интегрирования. Пусть известно давление 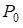 насыщенного пара при некоторой температуре
насыщенного пара при некоторой температуре 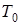 . Находим из (13.15):
. Находим из (13.15):
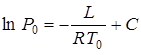 . (13.16)
. (13.16)
Вычитая (13.16) из (13.15), получим после потенцирования:
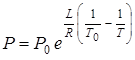 . (13.17)
. (13.17)
Задача 13.4. Давление насыщенного пара ртути зависит от температуры по закону
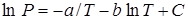 , (13.18)
, (13.18)
где 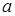 ,
, 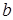 ,
, 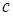 - постоянные. Найти скрытую молярную теплоту испарения ртути
- постоянные. Найти скрытую молярную теплоту испарения ртути 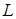 как функцию температуры.
как функцию температуры.
Ответ: 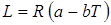 .
.
Указание.Продифференцировать (13.18) и определить 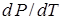 . Воспользоваться равенством (13.14).
. Воспользоваться равенством (13.14).
Дата добавления: 2015-02-05; просмотров: 11430;
