Чувствительность параметров
Чувствительностью системы называется выходных характеристик или показателей качества в зависимости от изменений параметров системы. Если система не изменяет свои выходные характеристики или показатели качества при изменении параметров системы, то такая система называется грубая (рабастая).
Количественной характеристикой чувствительности системы является функция чувствительности, которая определяется как частная производная какой-либо характеристики системы (передаточная, переходная характеристика, время переходного процесса и т.д.) по варьируемому параметру.
 , расчетное значение данного параметра.
, расчетное значение данного параметра.
Чаще всего на практике применяется относительная функция чувствительности:
 .
.
Чем меньше функция чувствительность (относительная функция чувствительности), тем грубее система и, следовательно, лучше качество управления.
 Для типовой системы: относительная ФЧ определяется следующей формулой:
Для типовой системы: относительная ФЧ определяется следующей формулой:
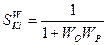 .
.

Типовые законы регулирования линейных систем
Рассмотрим типовые алгоритмы управления (законы регулирования), применяемые в линейных автоматических системах.
1. П (пропорциональный) – регулятор:
Простейший закон регулирования реализуется при помощи безынерционного звена с передаточной функцией
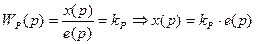 .
.
Согласно этому выражению, управляющее воздействие и в статике и в динамике пропорционально сигналу ошибки е. Поэтому такой закон регулирования называется пропорциональным (П).
Преимуществами данного регулятора являются простота и быстродействие, а недостатком – ограниченная точность.
2.И (интегральный) – регулятор:
Закон регулирования, которому соответствует передаточная функция
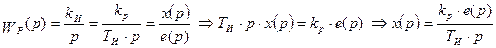 ,
,
где ТИ – постоянная времени регулятора.
Здесь управляющее воздействие у в каждый момент времени пропорционально интегралу от сигнала ошибки е. Поэтому И - регулятор реагирует главным образом на длительные отклонения управляемой величины от заданного значения. Кратковременные отклонения сглаживаются таким регулятором.
Преимуществом данного регулятора является лучшая по сравнению с П - регулятором точность установки режима, а недостатками – худшие по сравнению с П - регулятором показатели качества, а именно большая колебательность и меньшее быстродействие.
3.ПИ – регулятор:
Наибольшее распространение в промышленной автоматике получил пропорционально-интегральный (ПИ) закон регулирования
 .
.
Объединяет два регулятора П и И, следовательно, обладает наилучшими свойствами по сравнению с вышеописанными регуляторами, а именно: за счет П - составляющей улучшается показательные качества в переходном процессе, а за счет И - составляющей уменьшается ошибка регулирования ® т.е. улучшается точность.
4.Д (дифференциальный) – регулятор:
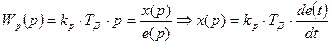 ,
,
где ТД – постоянная времени Д – регулятора.
Преимуществом данного регулятора является то, что х(р) зависит от дифференциальной ошибки, и регулятор реагирует на малейшее изменение ошибки. Однако очень большим недостатком является плохая помехоустойчивость (очень чувствительный). На практике практически не используется в чистом виде - как и идеальное дифференцирующее звено.
5. ПД – регулятор:
Наилучшее быстродействие достигается при пропорционально - дифференциальном (ПД) законе регулирования
 .
.
ПД – регулятор реагирует не только на величину сигнала ошибки, но и на скорость его изменения. Благодаря этому при управлении достигается эффект упреждения. Недостатком пропорционально – дифференциального закона регулирования является ограниченная точность.
6.ПДИ – регулятор:
Наиболее гибким законом регулирования (в классе линейных законов) является пропорционально – интегрально – дифференциальный (ПИД) закон
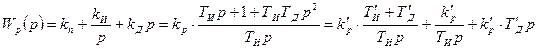 ,
,
который сочетает в себе преимущества более простых законов. Объединяет три регулятора П, И и Д, обладает преимуществами всех регуляторов, а недостатком является сложность реализации.
Дата добавления: 2015-02-16; просмотров: 928;
