Законы коммутации. Переходный процесс − это процесс, возникающий в электрической цепи, при переходе от одного установившегося режима к другому

Переходный процесс − это процесс, возникающий в электрической цепи, при переходе от одного установившегося режима к другому. Этот переход может быть вызван различными причинами:

− изменением структуры цепи (исключением отдельных элементов цепи или включением в цепь новых элементов);

− изменением параметров источников (например, изменением величины постоянной ЭДС, изменением амплитуды, частоты или фазы переменной ЭДС);

− изменением параметров элементов цепи (например, изменением числа витков катушки индуктивности).

Переходный процесс имеет место, например, при подключении какой-либо электрической цепи к источнику питания, или в случае возникновения аварийных ситуаций − выхода из строя какого-либо элемента, короткого замыкания и т.п. Причину возникновения переходного режима принято называть коммутацией, причем время ∆t, в течение которого она происходит, бесконечно мало, т.е. ∆t=0. Момент времени, предшествующий коммутации, обозначают t₋₀ , а момент времени, непосредственно прилегающей к коммутации, но после ее осуществления, обозначают t₊₀. Аналогичными индексами обозначают токи и напряжения в цепи в соответствующие моменты времени, например, i₋₀, u₋₀ и i₊₀, u₊₀.

Возникновение переходного процесса связано с наличием в электрических цепях элементов, запасающих энергию электромагнитного поля − индуктивностей и емкостей. Если электрическая цепь содержит только активные сопротивления, то переходный процесс в цепи не возникает, а переход от одного установившегося режима к другому происходит мгновенно. Это связано с тем, что в индуктивности и емкости происходит накопление энергии, а при переходе из одного установившегося режима в другой происходит перераспределение энергии электрического поля в емкости и магнитного поля в индуктивности.

В любой электрической цепи не могут развиваться бесконечно большие напряжения или протекать бесконечно большие токи. Это потребовало бы источников энергии бесконечно большой мощности, что физически невозможно. Поэтому мгновенная мощность p − всегда величина конечная.

Если изменение энергии W в емкости или индуктивности во время коммутации за время ∆t→0 обозначим ∆W=W₊₀− W₋₀ , то получим:

∆W= p∆t→0, (6.1)

откуда следует равенство W₊₀=W₋₀.

Поскольку энергия магнитного поля в индуктивности W_L и электрического поля в емкости W_C соответственно равны:

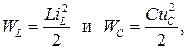
то, согласно выражению (6.1), изменения напряжения на емкости u_C и тока i_L в индуктивности в момент коммутации не происходит, т.е.

i_L−0= i_L+0 и u_C−0= u_C+0.

Полученные равенства выражают первый и второй законы коммутации:

Первый закон коммутации: ток через индуктивность непосредственно до коммутации равен току через ту же индуктивность после коммутации.

Второй закон коммутации: напряжение на емкости непосредственно до коммутации равно напряжению на той же емкости после коммутации.

Другими словами, ток в индуктивности и напряжение на емкости не могут меняться скачком.

Если говорить в более обобщенном смысле о процессе коммутации, то переходный режим также может возникать и при скачкообразном изменении как емкости, так и индуктивности при наличии индуктивной связи между контурами. Поэтому строго говоря в момент коммутации не может скачком измениться суммарное потокосцепление обмоток и суммарный заряд на емкостях электрической цепи.

Величины i_L+0 и u_C+0 являются начальными значениями, от которых в переходном процессе происходит изменение тока в индуктивности и напряжения на емкости. Поскольку они соответствуют значениям установившегося режима до коммутации и соответственно не зависят от характера самой коммутации, то их принято называть независимыми начальными условиями.

В течение переходного процесса токи и напряжения на элементах цепи изменяются. Для расчета переходного процесса составляют уравнения по законам Кирхгофа для мгновенных значений токов и напряжений и решают их. Учитывая, что связь между токами и напряжениями на реактивных элементах выражается через производную 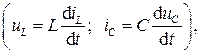расчет переходных режимов связан с решением дифференциальных уравнений. Порядок уравнения определяется числом реактивных элементов в цепи. Если в цепи имеется одна индуктивность или емкость, то получается уравнение первого порядка, а цепь называется цепью первого порядка. Если цепь содержит одну индуктивность и одну емкость, две индуктивности или две емкости, то получается уравнение второго порядка, а цепь называют цепью второго порядка, и т.д.

В связи с этим представляется целесообразным напомнить основные положения теории линейных дифференциальных уравнений.