Расчет цепей негармонического тока

Расчет цепей при периодических негармонических ЭДС и токах ведется по методу наложения. Последовательность расчета рассмотрим на примере цепи со смешанным соединением элементов R, L, C (рис. 5.1,а) и с источником, ЭДС e(t) которого изменяется по закону, соответствующему однополупериодному выпрямлению синусоидального напряжения с амплитудой E_m (рис. 5.1,б):

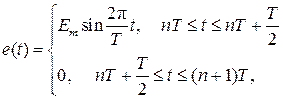
где n = 0,±1,±2,±3, ... ; T − период.

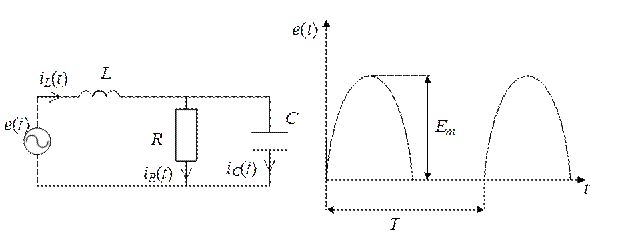
а) б)

Рис. 5.1. Цепь с негармоническим источником:

а) схема цепи; б) кривая ЭДС

Разложение несинусоидальной ЭДС в гармонический ряд имеет вид:

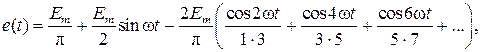(5.7)

где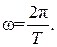

Какие члены в разложении учитывать при расчетах, определяется требуемой точностью. Кроме того, ряд, как правило, быстро убывает. Начиная с четвертого члена ряда, амплитуда гармоник составляет менее 5-10% от амплитуды первой гармоники. Поэтому для иллюстрации метода расчета рассмотрим только первые три члена ряда:

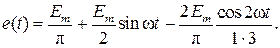
Как следует из последнего выражения, ЭДС или напряжение источника представляет собой совокупность ЭДС или напряжений трех источников: одного постоянного, величиной 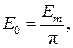и двух гармонических:

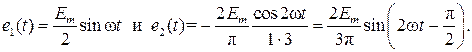
Гармонические ЭДС e₁(t) и e₂(t) называют соответственно первой и второй гармониками, а напряжение постоянного источника − постоянной составляющей ЭДС.

В соответствии с методом наложения необходимо произвести расчет цепи при каждом из воздействий. При этом для постоянной составляющей цепь следует рассматривать как цепь постоянного тока, а для гармоник − как цепь гармонического тока соответствующей частоты.

Таким образом, принципиально рассматриваются две схемы цепи: постоянного и переменного тока. Применительно к исходной цепи (рис. 5.1,а) они имеют вид, как на рис. 5.2.

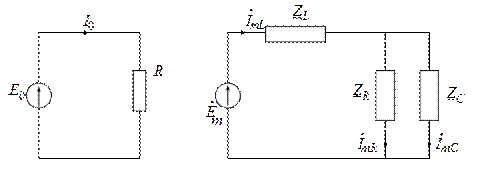
а) б)

Рис. 5.2. Расчетные схемы: а) для постоянной составляющей;

б) для гармонических составляющих

Цепь на рис. 5.2,а не содержит индуктивности и емкости, поскольку в установившемся режиме в цепи постоянного тока индуктивность эквивалентна сопротивлению с нулевым сопротивлением, а емкость эквивалентна разрыву цепи.

Цепь на рис. 5.2,б представляет собой изображение исходной цепи в комплексной области, поскольку расчет цепей гармонического тока ведется символическим методом. При этом для первой гармоники:

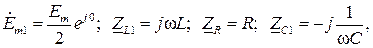
и для второй гармоники:

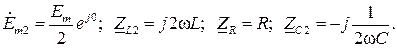
Расчет цепи как для постоянной составляющей, так и для гармоник ведется известными методами, изложенными в разделах 1 и 2 пособия, поэтому приведем только в общем виде выражения для токов в ветвях для каждой составляющей ЭДС:

− для постоянной составляющей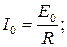

− для первой гармоники

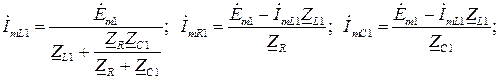
− для второй гармоники

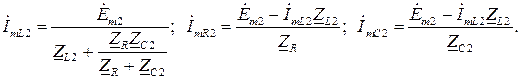
Переходя от комплексных амплитуд токов в ветвях к временным функциям, получим выражения для мгновенных токов в ветвях схемы:

− для первой гармоники:

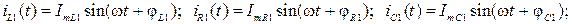
− для второй гармоники:

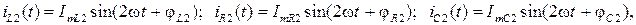где под начальными фазами гармонических функций (φ) понимаются аргументы соответствующих комплексных амплитуд токов.

Окончательно токи в ветвях при действии негармонической ЭДС будут представлять собой суммы соответствующих мгновенных токов:

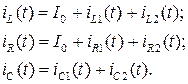
Для построения графиков токов в ветвях необходимо сложить ординаты постоянной составляющей и мгновенных значений всех рассчитанных гармоник.