Расчет цепей гармонического тока

Как указывалось выше, с использованием символического метода можно существенно упростить расчет цепей гармонического тока. Для иллюстрации сказанного рассмотрим методику расчета цепи с последовательным и параллельным соединением R, L, C и входным гармоническим напряжением u=U_m sin ωt.

1. Последовательное соединение R, L, C (рис. 2,5,а).

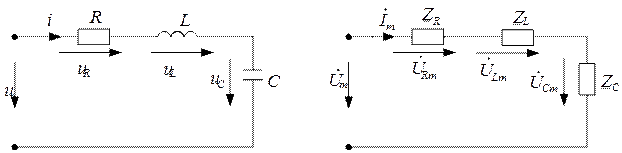
а) б)

Рис. 2.5. Расчетная схема: а) во временной области;

б) в комплексной области

Вначале осуществляют переход в комплексную область, изображая исходную схему с заменой всех величин их комплексными изображениями (рис. 2.5,б). Положительные направления тока и напряжений при этом на элементах цепи сохраняют во всех ветвях схемы.

По своему виду схема рис. 2.5,б напоминает резистивную цепь постоянного тока. Ее расчет можно вести любым известным методом расчета цепей постоянного тока, только с использованием комплексных изображений элементов и комплексных амплитуд напряжений и токов.

Для данной схемы с последовательным соединением элементов вначале найдем входное сопротивление 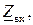которое равно сумме комплексных сопротивлений цепи

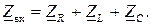
Тогда комплекс тока найдем из очевидного соотношения

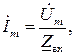
где 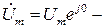комплексная амплитуда входного напряжения.

С учетом (2.4) получим

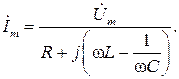
Для получения комплекса тока 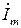произведем деление, переведя комплексное число в знаменателе в показательную форму,

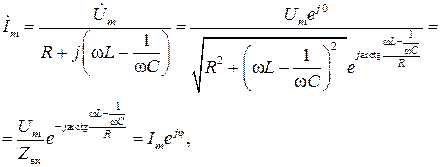
где 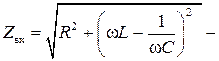модуль комплексного входного сопротивления; 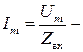- амплитуда тока в цепи, 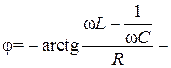фаза тока.

Комплекс входного сопротивления

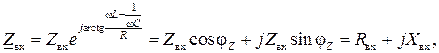(2.7)

где 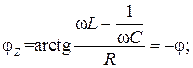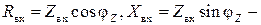соответственно активная и реактивная составляющие входного сопротивления.

Падение напряжения на каждом двухполюснике найдем с использованием (2.6)

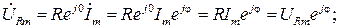
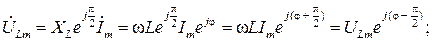
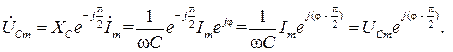
Переходя во временную область, найдем ток и падения напряжения на каждом элементе цепи при нулевой фазе входного напряжения :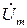

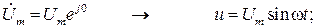
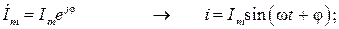
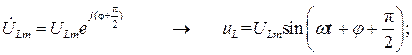
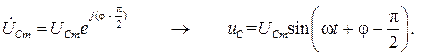
Таким образом, цепь гармонического тока рассчитана без применения операций дифференцирования, а лишь с использованием алгебраических действий в комплексной области.

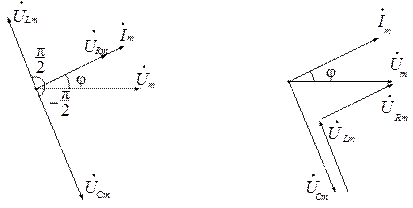
Изображая на комплексной плоскости вектора, соответствующие комплексам тока и напряжений, наглядно можно оценить фазовые сдвиги (рис. 2.6).

а) б)

Рис. 2.6. Векторная диаграмма для последовательной цепи:

а) фазовые соотношения между векторами;

б) сложение векторов напряжений в контуре цепи

Поскольку задача решалась в общем виде, для определенности примем, что напряжение 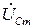(соответственно и реактивное сопротивление X_С) на емкости больше напряжения 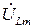(и реактивного сопротивления X_L) на индуктивности. Поэтому цепь по отношению к источнику носит активно-емкостной характер, и ток по фазе опережает напряжение источника на угол φ.

На векторной диаграмме (рис. 2.6,б) произведено сложение векторов напряжений двухполюсников в соответствии с ЗНК. При этом учитываются принятые в исходной схеме (рис. 2.5) положительные направления тока и напряжений на элементах цепи. Согласно ЗНК алгебраическая сумма падений напряжения в контуре равна нулю:

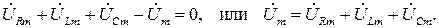
Таким образом, в комплексной форме законы Кирхгофа выполняются при условии учета фазовых сдвигов между напряжениями, которые должны складываться в векторной форме. Уместно отметить, что во временной области законы Кирхгофа выполняются для мгновенных значений:

u_R+u_L+u_C−u=0, или u= u_R+u_L+u_C.

2. Параллельное соединение R,L,C (рис. 2.7,а)

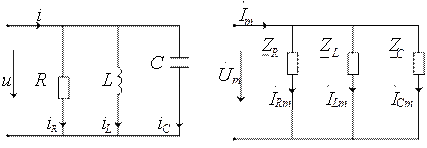
а) б)

Рис.2.7. Расчетная схема: а) во временной области;

б) в комплексной области

Переход в комплексную область осуществляется заменой всех величин их комплексными изображениями (рис. 2.7,б).

Ток в каждом двухполюснике определится по закону Ома:

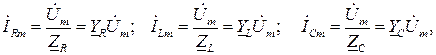(2.8)

где 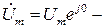комплексная амплитуда входного напряжения;

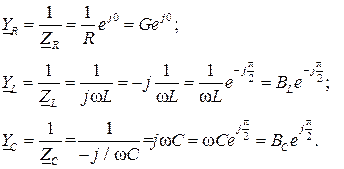
Здесь обозначено: 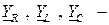комплексные проводимости сопротивления, индуктивности и емкости соответственно; 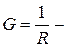активная проводимость; 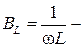реактивная проводимость индуктивности; 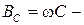реактивная проводимость емкости.

Ток 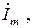потребляемый цепью, на основании ЗТК будет равен сумме токов двухполюсников: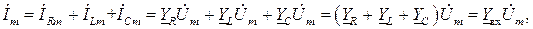

откуда следует, что комплексная входная проводимость цепи 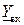равна сумме комплексных проводимостей параллельно соединенных элементов.

Подставляя в последнее выражение значения комплексных проводимостей, запишем

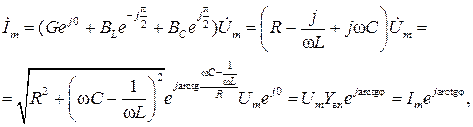
где 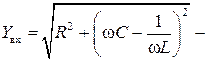модуль комплексной входной проводимости; 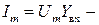амплитуда входного тока; 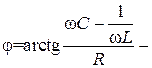фаза тока.

В соответствии с (2.8) запишем выражения для токов в ветвях:

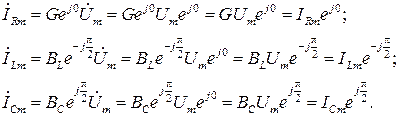
Переходя во временную область, найдем токи в ветвях цепи при нулевой фазе входного напряжения :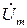

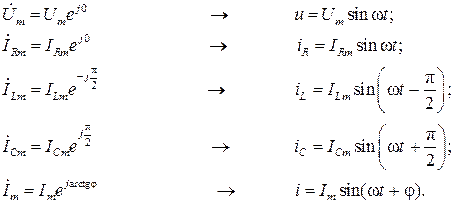
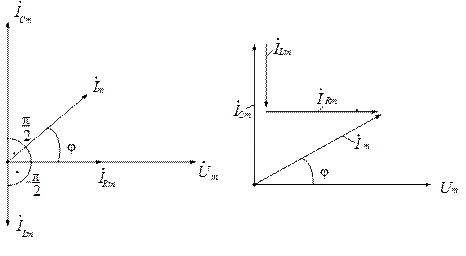
Изображая на комплексной плоскости вектора, соответствующие комплексам входного напряжения и токов в ветвях цепи, наглядно можно оценить фазовые сдвиги (рис. 2.8).

Поскольку задача решалась в общем виде, то здесь принято, что ток в емкости 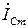(соответственно и реактивная проводимость B_C) , больше тока 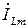(и реактивной проводимости B_L) в индуктивности. Поэтому цепь по отношению к источнику носит активно-емкостной характер, и ток по фазе опережает напряжение источника на угол φ.

а) б)

Рис. 2.8. Векторная диаграмма для параллельной цепи:

а) фазовые соотношения между векторами;

б) сложение векторов токов в ветвях цепи

На векторной диаграмме (рис. 2.8,б) произведено сложение векторов токов двухполюсников в соответствии с ЗТК. При этом учитываются принятые в исходной схеме (рис. 2.7) положительные направления токов в ветвях. Согласно ЗТК алгебраическая сумма токов в узле равна нулю:

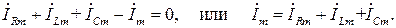
Таким образом, в комплексной форме ЗТК выполняется при условии учета фазовых сдвигов между токами, которые должны складываться в векторной форме. Уместно отметить, что во временной области ЗТК выполняется для мгновенных значений:

i_R+i_L+i_C−i=0, или i= i_R+i_L+i_C.