Раздел 2. ПАССИВНЫЕ ДВУХПОЛЮСНИКИ

В ЦЕПЯХ ГАРМОНИЧЕСКОГО ТОКА

Краткие теоретические сведения

Основные понятия и определения

Электрический ток, меняющийся во времени, называют переменным током. Если изменения напряжений и токов в цепях происходят по гармоническому закону, то такие цепи называются цепями гармонического (синусоидального) тока. Вид кривой синусоидального тока показан на рис.2.1.

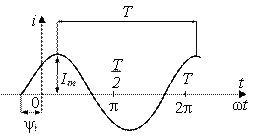
Рис.2.1.Кривая синусоидального тока

Ток записывается в виде синусоидальной функции:

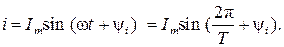
Максимальное значение функции I_m называют амплитудой тока; T − период изменения тока; ψ_i − начальная фаза тока. Частота тока − число колебаний за одну секунду: f=1/T, 1/с (Гц). Величину ω =2π/T называют угловой частотой и измеряют в рад./с. Аргумент синусоидальной функции (ωt + ψ_i) называют фазой. Текущее значение i называют мгновенным значением тока.

То же самое можно сказать и о синусоидальном напряжении:

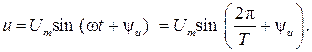
Очевидно, что в цепях гармонического тока частота тока и напряжения одинаковы, а вот начальные фазы могут отличаться. Рассмотрим рис. 2.2, где изображены кривые тока и напряжения.

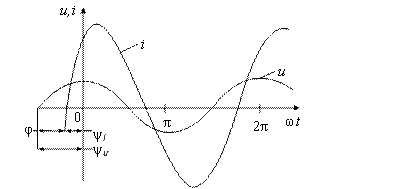
Рис.2.2. Кривые синусоидального тока и напряжения

В зависимости от того, в какой точке принято начало отсчета времени (начало координат на рис. 2.2), будут изменяться и начальные фазы тока и напряжения. Но разность фаз останется неизменной и равной φ. Поэтому при рассмотрении процессов в цепях гармонического тока начало координат при изображении кривых тока и напряжения совмещают с точкой перехода через ноль либо кривой напряжения, либо тока. Тогда начальная фаза одной из функций будет равна нулю, а другой φ. Так, если совместить на рис. 2.2 начало координат с точкой перехода через ноль тока, то выражения для тока и напряжения примут вид:

i=I_m sin ωt ; u=U_m sin (ωt + φ).

Если совместить начало координат с точкой перехода через ноль напряжения, то выражения для тока и напряжения примут вид:

i=I_m sin (ωt − φ) ; u=U_m sin ωt .

Для характеристики гармонического тока применяется понятие действующего значения (его называют также эффективным или среднеквадратичным). Под действующим значением тока I понимается постоянный ток, который оказывает такое же тепловое действие при прохождении через активное сопротивление, что и переменный ток:

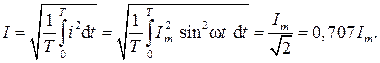
Аналогично определяют и действующее значение гармонического напряжения: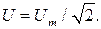

Отметим, что именно действующее значение измеряют приборы электромагнитной и электродинамической систем, которые используются при снятии показаний в лабораторных работах.

Рассмотрим, как ведут себя в цепях гармонического тока пассивные двухполюсники − элементы электрической цепи: активное сопротивление R, индуктивность L и емкость C.

При протекании тока по активному сопротивлению возникает падение напряжения, которое связано с мгновенным значением тока законом Ома:

u=Ri. (2.1)

Отсюда следует, что начальные фазы тока и напряжения совпадают, т.е. сдвиг фаз между током и напряжением равен нулю.

Индуктивность в цепи гармонического тока ведет себя иначе. При протекании тока по индуктивности возникает магнитное поле. Если ток переменный, то и магнитное поле (а следовательно, и магнитный поток) также изменяется во времени. На основании закона электромагнитной индукции переменный магнитный поток вызывает появление в индуктивности ЭДС самоиндукции, направленной против причины, вызвавшей ее появление. Математически данное утверждение выражается соотношением: 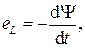где Ψ − потокосцепление, связанное с током i_L, протекающим по индуктивности, формулой Ψ=Li_L. Величина L носит название индуктивности и имеет размерность Гн (Генри). Для линейных цепей L=const, поэтому выражение для ЭДС самоиндукции примет вид

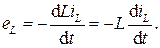
Этой ЭДС соответствует падение напряжения u_L, направленное в противоположную сторону, поэтому

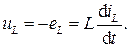(2.2)

Для гармонического тока i_L =I_m sin ωt , тогда

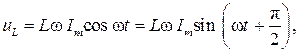
откуда следует, что разность фаз между напряжением и током составляет π/2, т.е. напряжение в индуктивности опережает по фазе ток на 90º. Величина Lω обозначается X_L, имеет размерность Ом и называется реактивным сопротивлением индуктивности.

Емкость представляет собой элемент электрической цепи, способный накапливать электрический заряд Q. При этом соотношение между величиной заряда и напряжением u_C на емкости имеет вид

Q=Cu_C .

Величина C носит название емкости и имеет размерность Ф (Фарад). Для линейных цепей C=const.

Если напряжение, приложенное к емкости, изменяется, то изменяется и накопленный в ней заряд. Как известно, изменение заряда означает протекание электрического тока. Тогда величину тока, протекающего через емкость, найдем из выражения

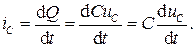(2.3)

Для гармонического напряжения u_С =U_m sin ωt, тогда получим

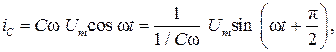
откуда следует, что разность фаз между напряжением и током составляет π/2, т.е. ток в емкости опережает по фазе напряжение на 90º. Величина 1/Cω обозначается X_С , имеет размерность Ом и называется реактивным сопротивлением емкости.