Основы символического метода

В цепях гармонического тока напряжения и ток в реактивных элементах связаны через операции дифференцирования и интегрирования. Поэтому расчеты установившихся режимов во временной области должны вестись путем решения дифференциальных уравнений, что в случае расчета сложных цепей приводит к трудно разрешимым проблемам. Переход в комплексную область позволяет свести расчеты цепей гармонического тока к решению алгебраических уравнений с использованием методов расчета цепей постоянного тока. Рассмотрим основы символического метода, который основан на символическом изображении действительных синусоидальных функций времени комплексными числами (этот метод иногда называют методом комплексных амплитуд).

Из курса математики известна формула Эйлера

e ^jα = cos α + jsin α.

Угол α в этой формуле может принимать любые значения. Положим α=ωt+ψ, тогда на основании формулы Эйлера запишем

e ^j(ωt+t) = cos (ωt+ψ) + jsin (ωt+ψ).

Согласно теории комплексных чисел последнее выражение представляет собой комплексное число, модуль которого равен единице, а аргумент является функцией времени. Умножим данное уравнение на I_m , тогда получим

I_m e ^j(ωt+ψ) = I_m cos (ωt+ψ) + j I_m sin (ωt+ψ).

Полученное выражение представляет собой комплексное число с модулем I_m и аргументом (ωt+ψ). На комплексной плоскости оно изображается в виде вектора длиной I_m , вращающегося против часовой стрелки с угловой частотой ω (рис.2.3). Тогда проекции вектора на оси координат представляют собой гармонические функции.

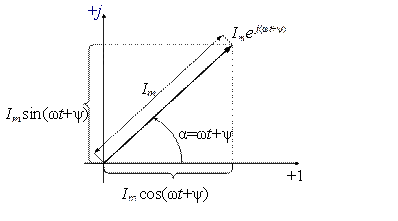
Рис.2.3. Изображение числа I_m e ^j(ωt+ψ) на комплексной плоскости

Как видно из рисунка, синусоидальный ток I_msin(ωt+ψ) может рассматриваться как проекция вектора I_m e ^j(ωt+ψ) на мнимую ось. Данное обстоятельство позволяет сделать вывод о взаимно-однозначном соответствии между гармонической функцией и комплексным числом, т.е.

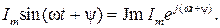
Отметим, что в радиотехнической литературе данное взаимно-однозначное соответствие устанавливается между косинусоидальной функцией и соответствующим комплексным числом, т.е.

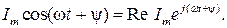
Если на комплексной плоскости изобразить другой вектор, например,

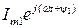, то он будет также вращаться с угловой частотой ω против часовой стрелки, но угол между этими векторами будет неизменным и равным разности начальных фаз ψ и ψ₁.

Представим число I_m e ^j(ωt+ψ) в виде произведения I_me^jψe ^jωt. Комплексное число I_me^jψ будет представлять собой вектор длиной I_m с аргументом ψ, неподвижный относительно координатной плоскости. Сомножитель e ^jωt носит название оператора вращения, поскольку умножение комплексного числа на него приводит к вращению вектора с частотой ω. Комплексное число I_me^jψ называют комплексной амплитудой.

То же самое можно сказать и для числа 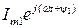. Тогда векторы, изображающие комплексные амплитуды I_me^jψ и 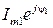, на комплексной плоскости будут неподвижны, а угол между ними будет равен разности начальных фаз ψ и ψ₁.

В цепях гармонического тока все напряжения и токи имеют одинаковую частоту, равную частоте источника, поэтому в уравнениях, описывающих процессы в электрических цепях в комплексном виде, сомножитель e ^jωt будет общим для всех членов соответствующих уравнений. Очевидно, его можно сократить. Тогда формальное взаимно-однозначное соответствие устанавливают между гармоническими функциями и их комплексными амплитудами. Комплексная амплитуда обозначается точкой вверху индекса: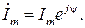

Математические действия над гармоническими функциями во временной области имеют свои соответствия в комплексной области. Не приводя строгих математических доказательств, дадим связь основных математических действий над гармоническими функциями во временной области с соответствующими им действиями в комплексной области над комплексными амплитудами.

Если x=X_msin(ωt+ψ_x) и y=Y_msin(ωt+ψ_y), то им соответствуют комплексные амплитуды 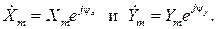Соответствующие действия над ними отражены в табл. 2.1.

Соответствие действий во временной и комплексной областях Таблица 2.1

Действие во временной области	Действие в комплексной области
kx, k - постоянное число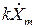
x±y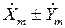
xy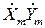
x/y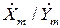

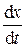
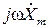
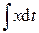
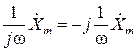
Действия над комплексными амплитудами производятся в соответствии с правилами действий над комплексными числами. Таким образом, дифференцирование и интегрирование во временной области в комплексной области заменяются алгебраическими операциями умножения и деления на комплексное число jω.