Резонанс в цепи гармонического тока

В общем случае двухполюсник в цепи гармонического тока содержит индуктивности, емкости и активные сопротивления. По отношению ко внешней цепи такой двухполюсник ведет себя как активно-индуктивная цепь, или активно-емкостная, в зависимости от того, какое из реактивных сопротивлений преобладает. Под резонансным режимом работы двухполюсника понимают режим, при котором его входное сопротивление является чисто активным, не смотря на наличие реактивных элементов. Отсюда следует, что условием возникновения режима резонанса является равенство нулю мнимой части входного сопротивления. В этом случае напряжение и ток на входе двухполюсника совпадают по фазе (cosφ=1), а реактивная мощность двухполюсника равна нулю (sinφ=0).

При рассмотрении резонанса будем оперировать с комплексами действующих значений напряжений и токов.

Различают резонанс напряжений и резонанс токов.

Резонанс напряжений имеет место в цепи с последовательным соединением R, L, C (рис. 2.9,а).

Комплекс входного сопротивления последовательной цепи

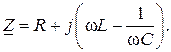
Условием резонанса является равенство нулю мнимой части 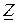, т.е.

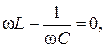
откуда определяем резонансную частоту ω₀

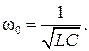(2.13)

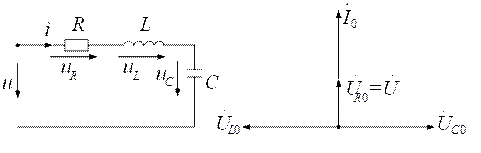
а) б)

Рис. 2.9. Схема с последовательным соединением элементов:

а) схема цепи; б) векторная диаграмма

при резонансе напряжений

Таким образом, режим резонанса можно достичь либо изменением частоты напряжения источника ω, либо изменением величины индуктивности L, либо изменением величины емкости С.

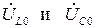При резонансе входное сопротивление цепи минимально и равно активному сопротивлению R, а ток достигает максимальной величины. Напряжения на реактивных элементах при резонансе одинаковы по величине и противоположны по фазе, поэтому на векторной диаграмме, изображающей напряжения на элементах (рис. 2.7,б), они компенсируют друг друга, а входное напряжение 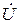равно падению напряжения на активном сопротивлении: 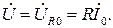При этом напряжения на индуктивности и емкости могут быть достаточно велики и превосходить входное напряжение.

Сопротивления реактивных элементов при резонансной частоте называют волновым сопротивлением ρ

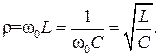
Отношение напряжения на реактивном сопротивлении при резонансе к приложенному напряжению называется добротностью Q

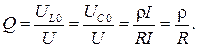
Обратное отношение называется затуханием цепи d

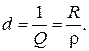
Добротность показывает, во сколько раз напряжение на индуктивности или на емкости превышает напряжение на входе схемы при резонансе. В радиотехнических устройствах Q может доходить до 300 и больше.

Поскольку при резонансе цепь ведет себя как чисто активная, энергия, поступающая от источника, покрывает только потери энергии в активном сопротивлении. При этом происходит обмен запасенной энергией между емкостью и индуктивностью без возврата ее в источник.

Входное сопротивление последовательного контура является функцией частоты. Зависимости действительной и мнимой части входного сопротивления от частоты называют частотными характеристиками контура. Они позволяют определить поведение резонансного контура в окрестности резонансной частоты и оценить влияние добротности на его свойства. С частотными характеристиками можно ознакомиться в любом учебнике по ТОЭ или учебном пособии. В настоящем лабораторном практикуме для исследования резонанса используют источник с фиксированной частотой, а резонанс достигается изменением величины емкости. Поэтому рассмотрим, как изменяются входное сопротивление, напряжения на элементах и ток в цепи при изменении величины емкости.

Входное сопротивление двухполюсника

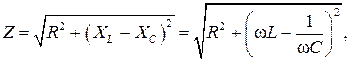(2.14)

а действующее значение тока в цепи

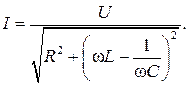
Здесь переменной величиной является емкость C.

Рассмотрим зависимости составляющих сопротивления Z в функции C (рис. 2.10). Активное сопротивление R и реактивное сопротивление индуктивности X_L с изменением емкости не меняются, поэтому их графики представляют собой прямые, параллельные оси абсцисс.

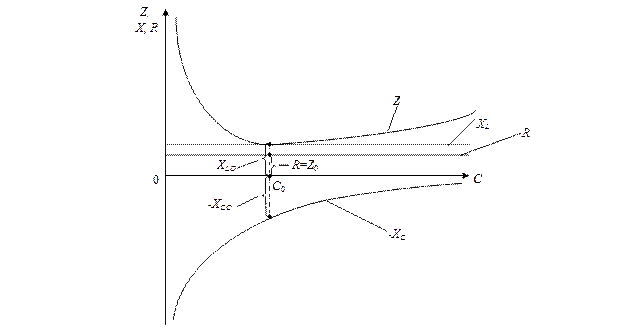
Рис. 2.10. Графики изменения сопротивлений контура

Реактивное сопротивление X_C=1/ωC в функции емкости изменяется в обратной пропорции. Суммируя ординаты кривых сопротивлений в соответствии с (2.14), получим график изменения входного сопротивления Z в функции емкости. При величине емкости C₀, соответствующей резонансной частоте, входное сопротивление достигает минимального значения Z₀=R. Очевидно, что кривая тока I будет иметь выраженный максимум в этой же точке (рис. 2.11).

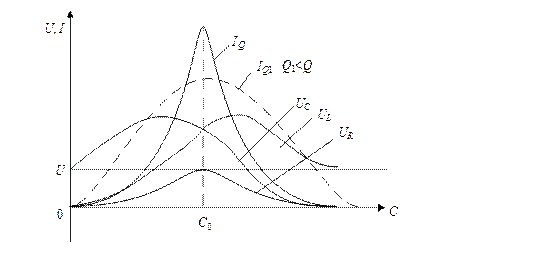
Рис.2.11. Резонансные кривые последовательного контура

Напряжение на активном сопротивлении U_R будет иметь максимум при резонансе.

Напряжение на емкости U_C будет изменяться от величины напряжения источника U при ω=0, как на рис. 2.11, через максимум до нуля при ω→∞.

Напряжение на индуктивности U_L будет меняться от нуля при ω=0 через максимум при резонансе до величины напряжения источника при ω→∞.

Форма кривой тока будет зависеть от добротности, т.е. от величины активного сопротивления. При меньшей добротности (Q1˂ Q) кривая тока I_Q1 (на рис. 2.11 изображена пунктиром) идет более полого, а ток при резонансной частоте меньше, чем при высокой добротности. Таким образом, чем больше добротность контура, тем более острой (пикообразной) становится форма кривой тока.

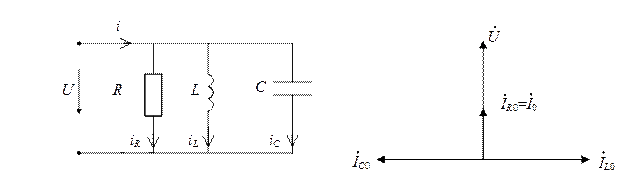
Резонанс токов имеет место в цепи с параллельным соединением R, L, C (рис. 2.12,а).

а) б)

Рис. 2.12. Схема с параллельным соединением элементов:

а) схема цепи; б) векторная диаграмма при резонансе токов

Комплекс входной проводимости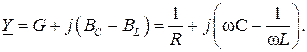

Условием резонанса является равенство нулю мнимой части 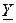, т.е.

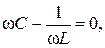
откуда определяем резонансную частоту ω₀

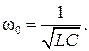
Таким образом, режим резонанса можно достичь либо изменением частоты напряжения источника ω, либо изменением величины индуктивности L, либо изменением величины емкости С.

При резонансе входная проводимость цепи минимальна и равна активной проводимости G, а ток I достигает минимального значения. Токи в реактивных элементах при резонансе 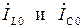одинаковы по величине и противоположны по фазе, поэтому на векторной диаграмме, изображающей токи в элементах (рис. 2.12,б), они компенсируют друг друга, а входной ток 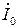равен току в активной проводимости 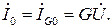При этом токи в реактивных элементах могут превосходить ток в неразветвленной части цепи.

Проводимости реактивных элементов при резонансной частоте называют волновой проводимостью γ

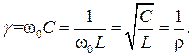
Отношение активной проводимости к волновой называется затуханием цепи d=g/γ. Затухание цепи с параллельным соединением равно также отношению тока I₀ в неразветвленной части цепи к току в индуктивности или емкости:

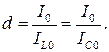
Чем меньше затухание контура, тем больше ток при резонансе в реактивных элементах по сравнению с током в неразветвленной цепи (входным током).

Резонансная кривая тока в параллельном контуре приведена на рис. 2.13. Такой же вид кривая тока имеет и в случае изменения величины емкости или индуктивности при неизменной частоте.

При резонансе токов также происходит обмен энергией между индуктивностью и емкостью, а энергия от источника покрывает только потери энергии в активном сопротивлении цепи. Электрические колебания в параллельных ветвях, обусловленные колебаниями энергии, могут быть очень интенсивными, а токи в реактивных элементах очень большими при относительно небольшом токе сети.

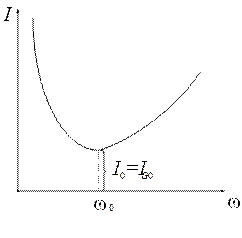
Рис. 2.13. Резонансная кривая тока

Для определения резонансной частоты при смешанном соединении элементов R, L, C необходимо найти комплекс входного сопротивления цепи и приравнять нулю его мнимую часть. Если в результате вычислений получается комплексное значение резонансной частоты, то резонанс при таком сочетании параметров невозможен.