Расчетная часть. 1. По данным табл. 2.3 следует рассчитать следующие параметры двухполюсников:

1. По данным табл. 2.3 следует рассчитать следующие параметры двухполюсников:

- активное сопротивление R16, реактивное сопротивление емкости X_C1 и реактивное сопротивление индуктивности X_L2 с использованием формул (2.6);

- фазовые сдвиги тока относительно напряжения каждого двухполюсника φ_R16, φ_C1, φ_L2 по формуле (2.12);

- емкость конденсатора C1 и индуктивность L2 с использованием формул (2.4), полагая частоту напряжения питания f=50 Гц.

Привести примеры вычислений. Результаты занести в табл. 2.4.

По данным расчетов в соответствующие графы табл. 2.4 записать комплексные сопротивления 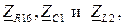используя показательную форму записи комплексного числа.

Данные вычислений Таблица 2.4

Сопротивление R16	Емкость C1	Индуктивность L2
R16, Ом	φR16, град.		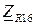XC1 , Ом	φС1, град.		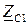С1, мкФ	XL2 , Ом	φL2, град.		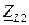L2, Гн

2. Построить на комплексной плоскости векторные диаграммы напряжения и тока для каждого двухполюсника. Указать выбранные масштабы напряжения и тока, обозначить фазовый сдвиг.

Содержание отчета

1. Титульный лист.

2. Цель и краткое содержание работы.

3. Принципиальная схема исследуемой цепи.

4. Таблицы с данными измерений и расчетов.

5. Расчеты параметров двухполюсников.

6. Векторные диаграммы токов и напряжений для каждого двухполюсника.

7. Ответы на контрольные вопросы.

Контрольные вопросы

1. Каковы основные характеристики синусоидальных токов и напряжений? Укажите их условные обозначения и единицы измерения.

2. Что такое сдвиг по фазе между током и напряжением, чем он обусловлен у индуктивности и емкости и почему он отсутствует у сопротивления?

3. В чем смысл и преимущество замены синусоидальных функций комплексными числами и соответствующими векторами на комплексной плоскости?

4. Как аналитически выражаются векторы на комплексной плоскости с помощью комплексных чисел в показательной и алгебраической форме?