Построение вероятностного пространства.
Последовательно строим вероятностное пространство.
Этап 1:
Имеется испытание. В результате проведения испытания может наблюдаться одно событие из серии событий e. Все события из системы e называются наблюдаемыми. Введем предположение, что если события A Ì e, B Ì e наблюдаемы, то наблюдаемы и события 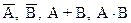 .
.
Система событий F называется полем событий или алгеброй событий, если для двух произвольных событий A, B Ì F выполняется:
1) Дополнения 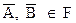
2) (A+B) Î F, (A×B) Î F
3) все конечные суммы элементов из алгебры принадлежат алгебре
4) все конечные произведения элементов из алгебры принадлежат алгебре
5) все дополнения конечных сумм и произведений принадлежат алгебре.
Таким образом, систему e мы расширяем до алгебры или поля F путем включения всех конечных сумм, произведений, и их дополнений. Т.е. считаем, что в результате проведения испытания наблюдаемая система является полем или алгеброй.
Множество всех подмножеств конечного числа событий является наблюдаемой системой - алгеброй, полем.
Этап 2:
Каждому событию A Î F ставим в соответствие число P(A), которое называется вероятностью наступления события A. Такая операция задает вероятностную меру.
Вероятностная мера - числовая скалярная функция, аргументами которой являются элементы из системы алгебры F. Введенная вероятностная мера удовлетворяет системе из трех аксиом.
1. 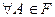
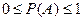
2. P(U)=1.
3. Рассмотрим конечную или бесконечную систему попарно несовместных событий, каждое из которых принадлежит алгебре F.
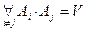 . Если
. Если 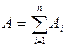 , то
, то 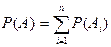 .
.
Алгебра событий называется s - алгеброй, если эта система событий содержит в себе все конечные суммы и произведения из алгебры F и их дополнения, а также все бесконечные суммы и произведения из алгебры и их дополнения.
Пример: В пространстве R1 зададим в качестве поля событий все конечные интервалы вида a³x>b, b¹a.
Распространение этой алгебры на s - алгебру приводит к понятию борелевской алгебры, элементы которой называются борелевскими множествами. Борелевская алгебра получается не только расширением поля вида a³x>b, но и расширением полей вида a>x³b, a³x³b.
Над наблюдаемым полем событий F задается счетно-аддитивная мера - числовая скалярная функция, элементами которой являются элементы поля F, т.е. события. Она удовлетворяет следующим трем условиям-аксиомам теории вероятности.
1. 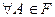
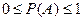 . P(A) - число, принадлежащее сегменту [0, 1] и называющееся вероятностью наступления события A.
. P(A) - число, принадлежащее сегменту [0, 1] и называющееся вероятностью наступления события A.
2. P(A) Î [0, 1] P(U)=1.
3. Пусть имеется A1, A2, A3,..., Ak - система попарно несовместных событий
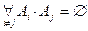 Если
Если 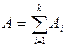 , то
, то 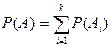 .
.
Дата добавления: 2015-02-16; просмотров: 555;
